
分析 分别构造函数g(x)=$\frac{f(x)}{{x}^{2}}$,x∈(0,+∞),h(x)=$\frac{f(x)}{{x}^{3}}$,x∈(0,+∞),利用导数研究其单调性即可得出.
解答 解:令g(x)=$\frac{f(x)}{{x}^{2}}$,x∈(0,+∞),
g′(x)=$\frac{xf′(x)-2f(x)}{{x}^{3}}$,
∵?x∈(0,+∞),2f(x)<xf′(x)<3f(x)恒成立,
∴f(x)>0,
0<$\frac{xf′(x)-2f(x)}{{x}^{3}}$,
∴g′(x)>0,
∴函数g(x)在x∈(0,+∞)上单调递增,
∴g(2)<g(3),即$\frac{f(2)}{4}$<$\frac{f(3)}{9}$,
∴$\frac{f(2)}{f(3)}$<$\frac{4}{9}$①,
令h(x)=$\frac{f(x)}{{x}^{3}}$,x∈(0,+∞),
h′(x)=$\frac{xf′(x)-3f(x)}{{x}^{4}}$,
∵?x∈(0,+∞),2f(x)<xf′(x)<3f(x)恒成立,
∴h′(x)=$\frac{xf′(x)-3f(x)}{{x}^{4}}$<0,
∴函数h(x)在x∈(0,+∞)上单调递减,
∴h(2)>g(3),即$\frac{f(2)}{8}$>$\frac{f(3)}{27}$,
∴$\frac{f(2)}{f(3)}$>$\frac{8}{27}$②,
∴综合①②:$\frac{8}{27}<\frac{f(2)}{f(3)}<\frac{4}{9}$,
故答案为:($\frac{8}{27}$,$\frac{4}{9}$).
点评 本题考查了利用导数研究其单调性极值与最值、构造函数法,考查了推理能力与计算能力,属于中档题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | 矩形的平行投影一定是矩形 | |
| B. | 梯形的平行投影一定是梯形 | |
| C. | 两条相交直线的投影可能平行 | |
| D. | 一条线段中点的平行投影仍是这条线段投影的中点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
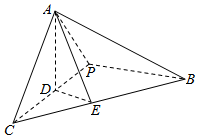 三棱锥A-PBC中,D是线段PC上一点,且AD⊥面BPC,AC=2,BC=3,AB=$\sqrt{7}$,E是BC上一点,且CE=1.
三棱锥A-PBC中,D是线段PC上一点,且AD⊥面BPC,AC=2,BC=3,AB=$\sqrt{7}$,E是BC上一点,且CE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数非偶函数 | B. | 偶函数非奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既非偶函数又非奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com