
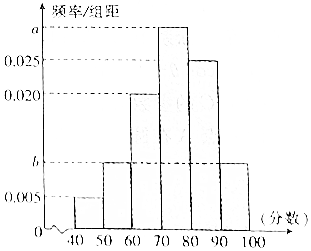
 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.分析 (Ⅰ)由直方图及等比数列性质求出b=0.030,由此能求出a.
(Ⅱ)由频率分布直方图能求出成绩不低于80分的人数.
(Ⅲ)两个分数段的学生分别为2人和4人,从6人中选2人,共有m=${C}_{6}^{2}=15$种等可能性选法,两人成绩差的绝对值大于10的选法有n=${C}_{2}^{1}•{C}_{4}^{1}=8$种选法,由此能求出这两名学生的数学成绩之差的绝对值大于10的概率.
解答 解:(Ⅰ)∵频率分布直方图中前三段的频率成等比数列.
∴由直方图及题意得(10b)2=0.05×0.20,
解得b=0.030,
∴a=0.1-0.005-0.010-0.020-0.025-0.010=0.030.
(Ⅱ)成绩不低于80分的人数估计为640×(0.025+0.010)×10=224.
(Ⅲ)两个分数段的学生分别为2人和4人,
从6人中选2人,共有m=${C}_{6}^{2}=15$种等可能性选法,
两人成绩差的绝对值大于10的选法有n=${C}_{2}^{1}•{C}_{4}^{1}=8$种选法,
∴这两名学生的数学成绩之差的绝对值大于10的概率:
p=$\frac{m}{n}=\frac{8}{15}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想,函数与方程思想、数形结合思想,是基础题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
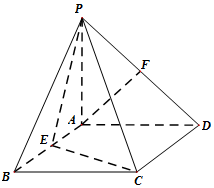 如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.
如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
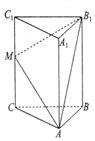 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(2x+$\frac{π}{6}$) | B. | y=sin2x | C. | y=sin(2x+$\frac{π}{3}$) | D. | y=sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
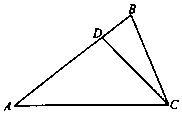 如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.
如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{4}π$ | B. | $\frac{25}{12}π$ | C. | $\frac{125}{48}π$ | D. | 25π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com