
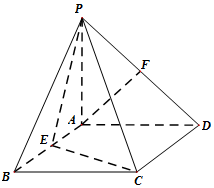
 如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.
如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.分析 (Ⅰ)取PC的中点G,连结FG、EG,AF∥EG又EG?平面PCE,AF?平面PCE,AF∥平面PCE;
(Ⅱ)由(Ⅰ)得EG∥AF,只需证明AF⊥面PDC,即可得到平面PEC⊥平面PCD.
解答 证明: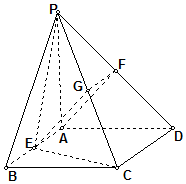 (Ⅰ)取PC的中点G,连结FG、EG,
(Ⅰ)取PC的中点G,连结FG、EG,
∴FG为△CDP的中位线,FG∥CD,FG=$\frac{1}{2}$CD.
∵四边形ABCD为矩形,E为AB的中点,∴AE∥CD,AE=$\frac{1}{2}$CD.
∴FG=AE,FG∥AE,∴四边形AEGF是平行四边形,
∴AF∥EG又EG?平面PCE,AF?平面PCE,
∴AF∥平面PCE;
(Ⅱ)∵PA=AD.∴AF⊥PD
PA⊥平面ABCD,∴PA⊥CD,
又因为CD⊥AB,AP∩AB=A,∴CD⊥面APD
∴CD⊥AF,且PD∩CD=D,∴AF⊥面PDC
由(Ⅰ)得EG∥AF,∴EG⊥面PDC
又EG?平面PCE,∴平面PEC⊥平面PCD.
点评 本题考查了空间线面平行、面面垂直的判定,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,6) | B. | [1,2) | C. | [2,4) | D. | (2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
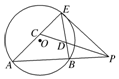 如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:
如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$:$\frac{π}{6}$:1 | B. | $\frac{π}{6}$:$\frac{π}{4}$:2 | C. | 1:3:$\frac{12}{π}$ | D. | 1:$\frac{3}{2}$:$\frac{6}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
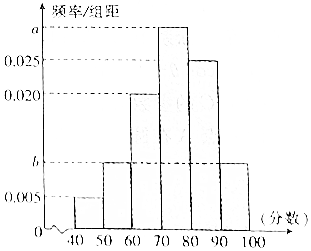 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥4 | B. | a≤4 | C. | a≥2$\sqrt{2}$ | D. | a≤2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com