
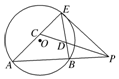
 如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:
如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:分析 (1)证明∠PEB=∠PAC,∠EPC=∠CPA,可得∠ECD=∠EDC,即可证明结论;
(2)证明△EPB∽△APE,得$\frac{PE}{PB}$=$\frac{PA}{PE}$,PC是∠APE的平分线,得$\frac{PA}{PE}$=$\frac{CA}{CE}$,即可证明结论.
解答 证明:(1)∵PE是⊙O的切线,
∴∠PEB=∠PAC,
∵PC是∠APE的平分线,
∴∠EPC=∠CPA,
∴∠PEB+∠EPC=∠PAC+∠CPA,
∴∠ECD=∠EDC,
∴DE=CE;
(2)∵∠PEB=∠PAC,∠EPB=∠APE,
∴△EPB∽△APE,
∴$\frac{PE}{PB}$=$\frac{PA}{PE}$,
∵PC是∠APE的平分线,
∴$\frac{PA}{PE}$=$\frac{CA}{CE}$,
∴$\frac{CA}{CE}=\frac{PE}{PB}$.
点评 本题考查圆的切线的性质,考查三角形相似的判定与性质,考查角平分线的性质,属于中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
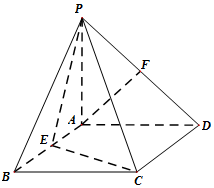 如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.
如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(2x+$\frac{π}{6}$) | B. | y=sin2x | C. | y=sin(2x+$\frac{π}{3}$) | D. | y=sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com