
分析 设O是O是△ABC的内任一点,以O为坐标原点,OA所在直线为x轴,建立直角坐标系.并设A(p,0),B(qcosα,sinα),C(rcosβ,-rsinβ),其中∠AOB=α,∠AOC=β,则∠BOC=2π-(α+β),利用向量的基本运算和不共线性质,即可求解证明.
解答 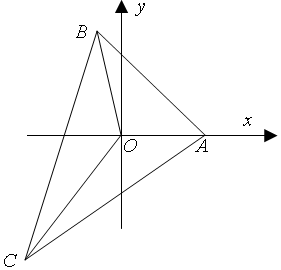 解:设O是△ABC的内任一点,以O为坐标原点,OA所在直线为x轴,建立直角坐标系.并设A(p,0),B(qcosα,qsinα),C(rcosβ,-rsinβ),其中∠AOB=α,∠AOC=β,则∠BOC=2π-(α+β),
解:设O是△ABC的内任一点,以O为坐标原点,OA所在直线为x轴,建立直角坐标系.并设A(p,0),B(qcosα,qsinα),C(rcosβ,-rsinβ),其中∠AOB=α,∠AOC=β,则∠BOC=2π-(α+β),
点O是△ABC的内心,显然$\overrightarrow{OB}$,$\overrightarrow{OC}$不共线,由平面向量基本定理,可得$\overrightarrow{OA}=x$$\overrightarrow{OB}$+y$\overrightarrow{OC}$.
则$\left\{\begin{array}{l}{P=xqcosα+yrcosβ}\\{0=xqsinα-yrsinβ}\end{array}\right.$,可得:$\left\{\begin{array}{l}{x=\frac{psinβ}{qsin(α+β)}}\\{y=\frac{psinα}{rsin(α+β)}}\end{array}\right.$
可得:$qrsin(α+β)\overrightarrow{OA}=prsinβ\overrightarrow{OB}+pqsinα\overrightarrow{OC}$,
∵SBOC:SAOB:sAOC=a:b:c,
即sinA:sinB:sinC=a:b:c.
∴sinA$\overrightarrow{OA}$+sinB$\overrightarrow{OB}$+sinC$\overrightarrow{OC}$=$\overrightarrow{0}$.
点评 本题考查了△ABC的内心的利用和向量的基本运算和不共线性质.属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
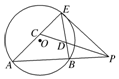 如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:
如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | $({-∞,\frac{1}{2}})$ | C. | $({\frac{1}{2},+∞})$ | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 女生 | 男生 | 合计 | |
| 喜欢吃甜食 | 8 | 4 | 12 |
| 不喜欢吃甜食 | 2 | 16 | 18 |
| 合计 | 10 | 20 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%的把握认为性别对喜欢吃甜食无影响 | |
| B. | 有99.5%的把握认为性别对喜欢吃甜食有影响 | |
| C. | 有99.9%的把握认为性别对喜欢吃甜食无影响 | |
| D. | 有99.9%的把握认为性别对喜欢吃甜食有影响 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -1 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥4 | B. | a≤4 | C. | a≥2$\sqrt{2}$ | D. | a≤2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
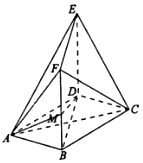 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com