
| A�� | $\frac{��}{4}$��$\frac{��}{6}$��1 | B�� | $\frac{��}{6}$��$\frac{��}{4}$��2 | C�� | 1��3��$\frac{12}{��}$ | D�� | 1��$\frac{3}{2}$��$\frac{6}{��}$ |
���� ������������ʽ���${k}_{1}=\frac{��}{6}$�����õȱ�Բ���������ʽ���${k}_{2}=\frac{��}{4}$������������������ʽ���k3=1���ɴ������k1��k2��k3��ֵ��
��� �⣺�����У�${V}_{1}=\frac{4}{3}��{R}^{3}$=$\frac{4}{3}�У�\frac{D}{2}��^{3}$=$\frac{��}{6}{D}^{3}$=${k}_{1}{D}^{3}$�����${k}_{1}=\frac{��}{6}$��
�ڵȱ�Բ���У�${V}_{2}=�У�\frac{D}{2}��^{2}$$•D=\frac{��}{4}•{D}^{3}$=${k}_{2}{D}^{3}$�����${k}_{2}=\frac{��}{4}$��
����������${V}_{3}={D}^{3}={k}_{3}{D}^{3}$�����k3=1��
��k1��k2��k3=$\frac{��}{6}��\frac{��}{4}��1$=1��$\frac{3}{2}$��$\frac{6}{��}$��
��ѡ��D��
���� ���⿼���ȱ�Բ����������ġ�����ʡ��ı�ֵ���������ȱ�Բ����������������ʽ�Ȼ���֪ʶ������������֤��������������������ռ��������������黯����ת��˼�룬�����뷽��˼�롢���ν��˼�룬���е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | $-\frac{3}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
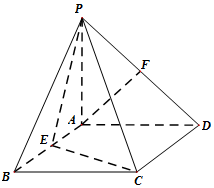 ��ͼ������P-ABCD�ĵ����Ǿ��Σ�PA��ƽ��ABCD��E��F�ֱ���AB��PD���е㣬��PA=AD��
��ͼ������P-ABCD�ĵ����Ǿ��Σ�PA��ƽ��ABCD��E��F�ֱ���AB��PD���е㣬��PA=AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
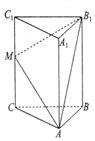 ��ͼ����������ABC-A1B1C1�У�CC1��ƽ��ABC��AC=BC=5��AB=6��M��CC1�е㣬CC1=8��
��ͼ����������ABC-A1B1C1�У�CC1��ƽ��ABC��AC=BC=5��AB=6��M��CC1�е㣬CC1=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=sin��2x+$\frac{��}{6}$�� | B�� | y=sin2x | C�� | y=sin��2x+$\frac{��}{3}$�� | D�� | y=sin��2x-$\frac{��}{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
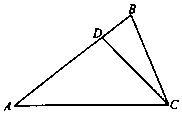 ��ͼ���ڡ�ABC�У���֪��D�ڱ�AB�ϣ�AD=3DB��cosA=$\frac{4}{5}$��cos��ACB=$\frac{5}{13}$��BC=13��
��ͼ���ڡ�ABC�У���֪��D�ڱ�AB�ϣ�AD=3DB��cosA=$\frac{4}{5}$��cos��ACB=$\frac{5}{13}$��BC=13���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com