
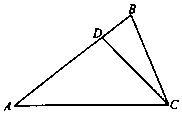
 如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.
如图,在△ABC中,已知点D在边AB上,AD=3DB,cosA=$\frac{4}{5}$,cos∠ACB=$\frac{5}{13}$,BC=13.分析 (1)在△ABC中,求出sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{3}{5}$.,sin∠ACB=$\frac{12}{13}$.
可得cosB=-cos(A+∠ACB)=sinAsin∠ACB-cosAcosB;
(2)在△ABC中,由正弦定理得,AB=$\frac{BC}{sinA}$sin∠ACB.
在△BCD中,由余弦定理得,CD=$\sqrt{B{D}^{2}+B{C}^{2}-2BD•BCcosB}$.
解答 解:(1)在△ABC中,cosA=$\frac{4}{5}$,A∈(0,π),
所以sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{3}{5}$.
同理可得,sin∠ACB=$\frac{12}{13}$.
所以cosB=cos[π-(A+∠ACB)]=-cos(A+∠ACB)
=sinAsin∠ACB-cosAcos∠ACB
=$\frac{3}{5}×\frac{12}{13}-\frac{4}{5}×\frac{5}{13}=\frac{16}{65}$;
(2)在△ABC中,由正弦定理得,AB=$\frac{BC}{sinA}$sin∠ACB=$\frac{13}{\frac{3}{5}}×\frac{12}{13}=20$.
又AD=3DB,所以DB=$\frac{1}{4}AB=5$.
在△BCD中,由余弦定理得,CD=$\sqrt{B{D}^{2}+B{C}^{2}-2BD•BCcosB}$
=$\sqrt{{5}^{2}+1{3}^{2}-2×5×13×\frac{16}{65}}$=9$\sqrt{2}$.
点评 本题考查了正余弦定理、三角恒等变形,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | [3,6) | B. | [1,2) | C. | [2,4) | D. | (2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$:$\frac{π}{6}$:1 | B. | $\frac{π}{6}$:$\frac{π}{4}$:2 | C. | 1:3:$\frac{12}{π}$ | D. | 1:$\frac{3}{2}$:$\frac{6}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
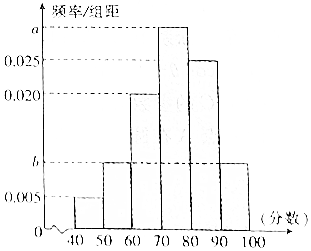 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | $({-∞,\frac{1}{2}})$ | C. | $({\frac{1}{2},+∞})$ | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (1,+∞) | C. | [0,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 女生 | 男生 | 合计 | |
| 喜欢吃甜食 | 8 | 4 | 12 |
| 不喜欢吃甜食 | 2 | 16 | 18 |
| 合计 | 10 | 20 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99.5%的把握认为性别对喜欢吃甜食无影响 | |
| B. | 有99.5%的把握认为性别对喜欢吃甜食有影响 | |
| C. | 有99.9%的把握认为性别对喜欢吃甜食无影响 | |
| D. | 有99.9%的把握认为性别对喜欢吃甜食有影响 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥4 | B. | a≤4 | C. | a≥2$\sqrt{2}$ | D. | a≤2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,3) | C. | (3,+∞) | D. | (-∞,4-e) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com