
 已知矩形ABCD中,AB=1,BC=$\sqrt{3}$,将此矩形按如图所示流程沿地面上一直线滚动,在滚动过程中,始终与地面垂直,设BC与地面所成角为θ,矩形周边上最高点离地面的距离为f(θ),求:
已知矩形ABCD中,AB=1,BC=$\sqrt{3}$,将此矩形按如图所示流程沿地面上一直线滚动,在滚动过程中,始终与地面垂直,设BC与地面所成角为θ,矩形周边上最高点离地面的距离为f(θ),求:分析 (1)根据BC与地面所成的角,是直线BC与平面所成的角,得出θ的取值范围;
(2)先求出∠DBC的大小,再作出图形,根据图形求出f(θ)的解析式;
(3)根据(2),结合三角函数的图象与性质,求出f(θ)的值域.
解答 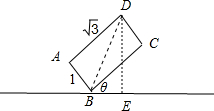 解:(1)BC与地面所成的角,是直线BC与地平面所成的角,
解:(1)BC与地面所成的角,是直线BC与地平面所成的角,
∴角θ的范围是[0,$\frac{π}{2}$];
(2)连接BD,Rt△BCD中,CD=AB=1,BC=AD=$\sqrt{3}$,
∴∠DBC=$\frac{π}{6}$;
过点D作地平面的垂线,垂足为E,如图所示;
在Rt△BDE中,∠DBE=θ+$\frac{π}{6}$,DB=2,
∴f(θ)=2sin(θ+$\frac{π}{6}$),(0≤θ≤$\frac{π}{2}$);
(3)由(2)知,当0≤θ≤$\frac{π}{2}$时,$\frac{π}{6}$≤θ+$\frac{π}{6}$≤$\frac{2π}{3}$,
∴$\frac{1}{2}$≤sin(θ+$\frac{π}{6}$)≤1,
∴1≤2sin(θ+$\frac{π}{6}$)≤2,
∴f(θ)的值域是[1,2].
点评 本题考查了三角函数的图象与性质的应用问题,也考查了数学建模的应用问题,是基础题目.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图是某中学参加高三体育考试的学生中抽取60名学生的体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图中的信息回答下列问题:
如图是某中学参加高三体育考试的学生中抽取60名学生的体育成绩(均为整数)的频率分布直方图,该直方图恰好缺少了成绩在区间[70,80)内的图形,根据图中的信息回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
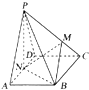 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com