
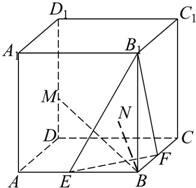
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.分析 (1)设BE=x,BF=y,把△B1EF的三边用含有a与x的代数式表示,利用余弦定理求得∠EB1F的余弦值,则其范围可求;
(2)设EF与BD的交点为G,连接B1G,可得∠B1GB为二面角B1-EF-B的平面角,求解直角三角形得答案;
(3)设EF与BD的交点为G,连接B1G,则由已知可得EF⊥平面BB1D1D,于是平面B1EF⊥平面BB1D1D,在平面BB1D1D内过B作BK⊥B1G于K,延长后交D1D所在的直线于点M,则BM⊥平面B1EF,在平面BB1D1D内,由△B1BG∽△BDM,可得M为D1D的中点.
解答 解:(1)设BE=x,BF=y,则${B}_{1}E=\sqrt{{a}^{2}+{x}^{2}}$,${B}_{1}F=\sqrt{{a}^{2}+{y}^{2}}$,$EF=\sqrt{{x}^{2}+{y}^{2}}$,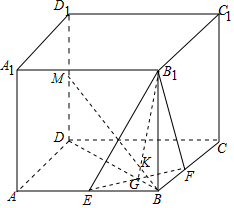
∴$cos∠E{B}_{1}F=\frac{2{a}^{2}}{2\sqrt{{x}^{2}+{a}^{2}}\sqrt{{y}^{2}+{a}^{2}}}<1$,
∴∠EB1F的取值范围为(0,$\frac{π}{2}$);
(2)设EF与BD的交点为G,连接B1G,
∵E、F分别为AB、BC的中点,∴BG⊥EF,B1G⊥EF,
则∠B1GB为二面角B1-EF-B的平面角.
由Rt△BAD∽Rt△BGE,得$\frac{BG}{AB}=\frac{BE}{BD}$,得$BG=\frac{BE•AB}{BD}=\frac{\frac{a}{2}•a}{\sqrt{2}a}=\frac{\sqrt{2}}{4}a$,
∴$tan∠{B}_{1}GB=\frac{a}{\frac{\sqrt{2}}{4}a}=2\sqrt{2}$,则$∠{B}_{1}GB=arctan2\sqrt{2}$;
(3)设EF与BD的交点为G,连接B1G,则由EF⊥BD,EF⊥B1B,BD∩B1B=B,
得EF⊥平面BB1D1D,于是平面B1EF⊥平面BB1D1D,
在平面BB1D1D内过B作BK⊥B1G于K,延长后交D1D所在的直线于点M,则BM⊥平面B1EF,
在平面BB1D1D内,由△B1BG∽△BDM,可得$\frac{{B}_{1}B}{BG}=\frac{BD}{DM}$,
又B1B=a,BG=$\frac{\sqrt{2}}{4}a$,BD=$\sqrt{2}a$,∴DM=$\frac{a}{2}$.
∴M在正方体棱D1D上,且恰好为D1D的中点.
点评 本题考查二面角的平面角及其求法,考查了空间想象能力和思维能力,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($\frac{π}{2}$)<f($\frac{π}{6}$)<f(0) | B. | f(0)<f($\frac{π}{2}$)<f($\frac{π}{6}$) | C. | f($\frac{π}{6}$)<f(0)<f($\frac{π}{2}$) | D. | f($\frac{π}{2}$)<f(0)<f($\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $-\frac{1}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
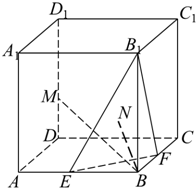 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | x=1是x2-3x+2=0的充分不必要条件 | |
| C. | 若“p或q”为假命题,则非p为真命题 | |
| D. | 对于命题p:存在x>0,使得x2-3x+2<0,则非p:任意x≤0,使x2-3x+2≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {1} | C. | $\{-1,\frac{{\sqrt{2}}}{2}\}$ | D. | $\{\frac{{\sqrt{2}}}{2}\}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com