
分析 (I)由已知向量等式可得$|\overrightarrow{AD}|=\frac{1}{2}$,$|\overrightarrow{BD}|=\frac{3}{2}$,由此求得$|\overrightarrow{AB}|$,得到A,B的坐标,设出双曲线方程及C,E的坐标,结合3$\overrightarrow{BE}$=2$\overrightarrow{EC}$,把E的坐标用C的坐标表示,代入双曲线方程求得a,b的值,则双曲线方程可求;
(II)设出M坐标,由已知条件得|TM|=|TN|,结合M,N在双曲线上可得7(x1+x2)=2x0,结合M,N的横坐标的范围求得T点横坐标x0取值范围.
解答 解:(I)由题知:$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}|}=\frac{1}{2}$ ①,而$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}|•|\overrightarrow{AC}|cosA$ ②,
由①②,$|\overrightarrow{AC}|cosA=\frac{1}{2}$,作CD⊥AB于D,即$|\overrightarrow{AD}|=\frac{1}{2}$.
同理,$|\overrightarrow{BD}|=\frac{3}{2}$,∴$|\overrightarrow{AB}|=2$,A(-1,0),B(1,0),
设双曲线方程$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$,$C(-\frac{1}{2},h)$,E(x1,y1),
由$3\overrightarrow{BE}=2\overrightarrow{EC}$,得$\left\{\begin{array}{l}{{x}_{1}=\frac{2}{5}}\\{{y}_{1}=\frac{2}{5}h}\end{array}\right.$,
∵E,C两点在双曲线上,∴$\left\{\begin{array}{l}{\frac{1}{4{a}^{2}}-\frac{{h}^{2}}{{b}^{2}}=1}\\{\frac{4}{25{a}^{2}}-\frac{4{h}^{2}}{25{b}^{2}}=1}\\{{c}^{2}={a}^{2}+{b}^{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=\frac{1}{7}}\\{{b}^{2}=\frac{6}{7}}\end{array}\right.$,
∴双曲线方程为$\frac{{x}^{2}}{\frac{1}{7}}-\frac{{y}^{2}}{\frac{6}{7}}=1$;
(II)设M(x1,y1),N(x2,y2),由条件知|TM|=|TN|,
得$\sqrt{{{y}_{1}}^{2}+({x}_{1}-{x}_{0})^{2}}=\sqrt{{{y}_{2}}^{2}+({x}_{2}-{x}_{0})^{2}}$,
∴${{y}_{1}}^{2}-{{y}_{2}}^{2}=({x}_{2}-{x}_{0})^{2}-({x}_{1}-{x}_{0})^{2}=({{x}_{2}}^{2}-{{x}_{1}}^{2})$+2x0(x1-x2) ①,
又M,N在双曲线上,满足$7{{x}_{1}}^{2}-\frac{7}{6}{{y}_{1}}^{2}=1$,$7{{x}_{2}}^{2}-\frac{7}{6}{{y}_{2}}^{2}=1$,
∴${{y}_{1}}^{2}-{{y}_{2}}^{2}=6({{x}_{1}}^{2}-{{x}_{2}}^{2})$ ②,
将②代入①,$7({{x}_{1}}^{2}-{{x}_{2}}^{2})=2{x}_{0}({x}_{1}-{x}_{2})$,由条件知x1≠x2,
∴7(x1+x2)=2x0,
又x1>$\frac{\sqrt{7}}{7}$,x2>$\frac{\sqrt{7}}{7}$,x1≠x2,
∴${x}_{0}=\frac{7}{2}({x}_{1}+{x}_{2})$>$\sqrt{7}$,
∴x0的取值范围为($\sqrt{7}$,+∞).
点评 本题考查双曲线标准方程的求法,考查了双曲线的简单性质,训练了直线与双曲线位置关系的应用,属难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
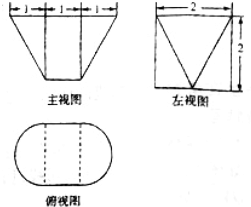 如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )
如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )| A. | 6+$\frac{2π}{3}$ | B. | 8+$\frac{π}{3}$ | C. | 4+$\frac{2π}{3}$ | D. | 4+$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S=1+2+3+…+10000000 | B. | S=1+2+3+4 | ||
| C. | S=1+2+3+…+n(n≥2且n∈N) | D. | S=12+22+32+…+1002 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
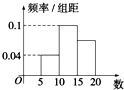 如图是一组样本数据的频率分布直方图,则依据图形中的数据,可以估计总体的平均数与中位数分别是( )
如图是一组样本数据的频率分布直方图,则依据图形中的数据,可以估计总体的平均数与中位数分别是( )| A. | 12.5,12.5 | B. | 13.5,13 | C. | 13.5,12.5 | D. | 13,13 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
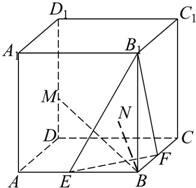 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com