
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | x=1是x2-3x+2=0的充分不必要条件 | |
| C. | 若“p或q”为假命题,则非p为真命题 | |
| D. | 对于命题p:存在x>0,使得x2-3x+2<0,则非p:任意x≤0,使x2-3x+2≥0 |
分析 直接写出命题的逆否命题判断A;由充分必要条件的判定方法判断B;由复合命题的真假判断判断C;写出特称命题的否定判断D.
解答 解:命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,故A正确;
若x=1,则x2-3x+2=0,反之,x2-3x+2=0,得x=1或x=2,∴x=1是x2-3x+2=0的充分不必要条件,故B正确;
若“p或q”为假命题,则p、q均为假命题,可得非p为真命题,故C正确;
对于命题p:存在x>0,使得x2-3x+2<0,则非p:任意x>0,使x2-3x+2≥0,故D错误.
故选:D.
点评 本题考查命题的真假判断与应用,考查了命题的逆否命题,考查复合命题的真假判断及充分必要条件的判定方法,是中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
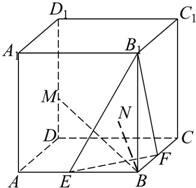 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、M分别是棱AB、BC和DD1 所在直线上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+2$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 1+2$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 30° | C. | 90° | D. | 45°或135° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com