
分析 (Ⅰ)运用数列的递推式:当n=1时,a1=S1,n>1时,an=Sn-Sn-1,化简计算即可得到所求通项公式;
(Ⅱ)由a1=1时,知${a_n}={2^{n-1}}$,求得${b_n}={2^n}+{({-1})^n}(n-1)$,运用数列的求和方法:分组求和,结合等比数列的求和公式,化简计算即可得到所求和.
解答 解:(Ⅰ)当n≥2时,Sn=2an-λ.①,Sn-1=2an-1-λ②
①-②可得an=2an-1(n≥2),
当n=1时,a1=λ,当n=2时,a2=2a1=2λ,
故数列{an}的通项公式为${a_n}=λ{2^{n-1}}$.
(Ⅱ)由a1=1时,知${a_n}={2^{n-1}}$,
故${b_n}={2^n}+{({-1})^n}(n-1)$,记数列{bn}的前2n项和为T2n,
T2n=(21-0)+(22+1)+(23-2)+…+[22n++(2n-1)]
=(2+22+23+…+22n)+(-0+1-2+3-…+2n-1)
=$\frac{2(1-{2}^{2n})}{1-2}$+(1+1+…+1)=22n+1-2+n.
故数列{bn}的前2n项和为22n+1-2+n.
点评 本题考查数列的通项公式的求法,注意运用数列递推式,考查数列的求和方法:分组求和,注意运用等比数列求和公式,属于中档题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | $16\sqrt{3}$ | C. | 32 | D. | $32\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
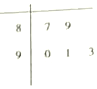 2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )
2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )| A. | 9 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com