
分析 (Ⅰ)由于f(x)为定义在R上的奇函数,则f(0)=0,可得a=1,再运用定义,检验f(x)为奇函数即可;
(Ⅱ)判断出y=f(x)在(0,+∞)上为增函数,由f(x)为奇函数,且过原点,可得f(x)在R上递增,f(2x)≤f($\frac{6}{lo{g}_{2}(x+1)}$-4)≤ln(3+$\sqrt{10}$)=f(3)?2x≤$\frac{6}{lo{g}_{2}(x+1)}$-4≤3,解不等式即可得到所求解集;
(Ⅲ)由题意结合f(x)为奇函数,f(x)在R上递增,可得f(a•4x+a)>f(-2x-1),a•4x+a>-2x-1,即a>$-\frac{{2}^{x}+1}{{4}^{x}+1}$.设t=2x+1(3≤t≤5),则2x=t-1,运用单调性求得最大值,即可得到a的范围.
解答 解:(Ⅰ)由于f(x)为定义在R上的奇函数,
则f(0)=0,即有ln$\sqrt{a}$=0,
解得a=1.
则有f(x)=ln(x+$\sqrt{1+{x}^{2}}$),
由x+$\sqrt{1+{x}^{2}}$>0,解得x∈R,
f(-x)+f(x)=lg(-x+$\sqrt{1+{x}^{2}}$)+lg(x+$\sqrt{1+{x}^{2}}$)=lg(x2+1-x2)=lg1=0,
即有f(-x)=-f(x),
则f(x)为奇函数.
故a=1;
(Ⅱ)设x1,x2∈(0,+∞),且x1<x2,
则f(x1)-f(x2)=$ln\frac{{x}_{1}+\sqrt{1+{{x}_{1}}^{2}}}{{x}_{2}+\sqrt{1+{{x}_{2}}^{2}}}$,
∵0<x1<x2,∴$\sqrt{1+{{x}_{1}}^{2}}<\sqrt{1+{{x}_{2}}^{2}}$,
则0<$\frac{{x}_{1}+\sqrt{1+{{x}_{1}}^{2}}}{{x}_{2}+\sqrt{1+{{x}_{2}}^{2}}}$<1,即$ln\frac{{x}_{1}+\sqrt{1+{{x}_{1}}^{2}}}{{x}_{2}+\sqrt{1+{{x}_{2}}^{2}}}$<0,
∴f(x1)<f(x2),则y=f(x)在(0,+∞)上为增函数,
由f(x)为奇函数,且过原点,可得f(x)在R上递增,
∴f(2x)≤f($\frac{6}{lo{g}_{2}(x+1)}$-4)≤ln(3+$\sqrt{10}$)=f(3),
?2x≤$\frac{6}{lo{g}_{2}(x+1)}$-4≤3,
首先log2(x+1)>0,即x>0.
即有(4+2x)log2(x+1)≤6,
由y=(4+2x)log2(x+1)的导数为y′=2xln2•log2(x+1)+(4+2x)•$\frac{1}{(x+1)ln2}$>0,
则x>0时,函数y递增,又x=1时,(4+2)log2(1+1)=6,
即有(4+2x)log2(x+1)≤6的解为0<x≤1①
$\frac{6}{lo{g}_{2}(x+1)}$-4≤3,即有log2(x+1)≥$\frac{6}{7}$,
解得x≥2${\;}^{\frac{6}{7}}$-1,②
由①②可得,2${\;}^{\frac{6}{7}}$-1≤x≤1.
则原不等式的解集为[2${\;}^{\frac{6}{7}}$-1,1];
(Ⅲ)不等式f(a•4x+a)+f(2x+1)>0?f(a•4x+a)>f(-2x-1),
∵y=f(x)在(0,+∞)上为增函数,且y=f(x)是定义在R上的奇函数,
∴y=f(x)在R上为增函数,
∴原不等式等价于a•4x+a>-2x-1,即a>$-\frac{{2}^{x}+1}{{4}^{x}+1}$.
设t=2x+1(3≤t≤5),则2x=t-1,
即有$-\frac{{2}^{x}+1}{{4}^{x}+1}$=-$\frac{t}{(t-1)^{2}+1}$=-$\frac{1}{t+\frac{2}{t}-2}$,
由t+$\frac{2}{t}$的导数为1-$\frac{2}{{t}^{2}}$>0,可得t+$\frac{2}{t}$在[3,5]递增,
可得t+$\frac{2}{t}$∈[$\frac{11}{3}$,$\frac{27}{5}$],即有-$\frac{1}{t+\frac{2}{t}-2}$∈[-$\frac{3}{2}$,-$\frac{5}{17}$].
则a>-$\frac{5}{17}$.
即有实数a的取值范围是(-$\frac{5}{17}$,+∞).
点评 本题考查了函数的单调性与奇偶性的判断与证明,考查了数学转化思想方法及分离变量法,训练了利用函数的单调性求函数的最值,是难题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
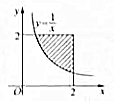 在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.
在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若?x≥0,有f(x)<0成立,则a<$\frac{1}{2}$ | B. | 若?x<0,f(x)≥0,则a<$\frac{1}{2}$ | ||
| C. | 若?x≥0,都有f(x)<0成立,则a<$\frac{1}{2}$ | D. | 若?x<0,有f(x)<0成立,则a<$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com