
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 根据平面向量的数量积运算公式,代入计算即可求出$\overrightarrow{a}$、$\overrightarrow{b}$的夹角.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,
且($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=1,
∴${\overrightarrow{a}}^{2}$-$\overrightarrow{b}$•$\overrightarrow{a}$=1,
∴22-3×2×cos<$\overrightarrow{b}$,$\overrightarrow{a}$>=1,
解得cos<$\overrightarrow{b}$,$\overrightarrow{a}$>=$\frac{1}{2}$,
∴$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$.
故选:C.
点评 本题考查了平面向量的数量积与夹角公式的计算问题,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
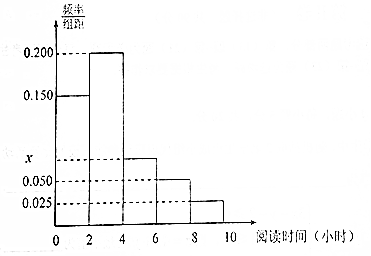 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 不喜欢戏剧 | 喜欢戏剧 | |
| 男性青年观众 | 40 | 10 |
| 女性青年观众 | 40 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{3}$ | B. | $\frac{40π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{80π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
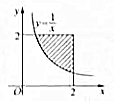 在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.
在平面直角坐标系内任取一个点P(x,y)满足$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$,则点P落在曲线y=$\frac{1}{x}$与直线x=2,y=2围成的阴影区域(如图所示)内的概率为$\frac{3-ln4}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com