
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 根据条件求出A,B的坐标,结合中点坐标公式建立a,c的关系进行求解即可.
解答 解:根据题意可求得A(c,$\frac{{b}^{2}}{a}$),B(c,$\frac{bc}{a}$),
∵2$\overrightarrow{OA}$=$\overrightarrow{OB}$+$\overrightarrow{OF}$,
∴A为BF的中点,∴2•$\frac{{b}^{2}}{a}$=$\frac{bc}{a}$,即c=2b,
∴双曲线C的离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{\frac{{c}^{2}}{{{c}^{2}-b}^{2}}}$=$\frac{2\sqrt{3}}{3}$,
故选:A
点评 本题主要考查双曲线离心率的计算,根据直线和双曲线的相交关系求出交点坐标,结合中点坐标公式以及离心率的公式是解决本题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
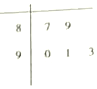 2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )
2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )| A. | 9 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
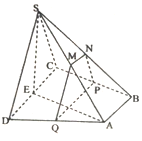 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别于BC,AD交于点P,Q,若|DQ|=λ|DA|查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com