
分析 (Ⅰ)由题意知$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{b=1}\end{array}\right.$⇒a=2,b=1,c=$\sqrt{3}$,即可;
(Ⅱ)(i)将直线y=k(x-4)(k≠0)代入椭圆C得:(1+4k2)x2-32k2x+64k2-4=0.则M(x1,k(x1-4)),N(x2,k(x2-4)).要证A,P,N三点共线,只证明$\overrightarrow{AP},\overrightarrow{AN}$共线即可,即证明$\frac{k({x}_{1}-4)}{{x}_{1}-2}({x}_{2}+2)=3k({x}_{2}-4)$成立.
(ii)将直线y=k(x-4)(k≠0)变形为x=my+4,(m=$\frac{1}{k}$).联立$\left\{\begin{array}{l}{x=my+1}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$得(m2-4)y2+8my-12=0.
|MN|=$\sqrt{1+{m}^{2}}\frac{4\sqrt{{m}^{2}-12}}{{m}^{2}+4}$,点O到直线MN的距离d=$\frac{4}{\sqrt{1+{m}^{2}}}$.△OMN面积S=$\frac{1}{2}$×|MN|×d即可.
解答 解:(Ⅰ)由题意知$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{b=1}\end{array}\right.$⇒a=2,b=1,c=$\sqrt{3}$,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(Ⅱ)(i)证明:将直线y=k(x-4)(k≠0)代入椭圆C得:(1+4k2)x2-32k2x+64k2-4=0.
$△=16(1-12{k}^{2})>0,解得-\frac{\sqrt{3}}{6}<k<\frac{\sqrt{3}}{6}$.
${x}_{1}+{x}_{2}=\frac{32{k}^{2}}{1+4{k}^{2}},{x}_{1}{x}_{2}=\frac{64{k}^{2}}{1+4{k}^{2}}$,…①
则M(x1,k(x1-4)),N(x2,k(x2-4)).
∴BM的方程为:$y=\frac{k({x}_{1}-4)}{{x}_{1}-2}(x-2)$,⇒P(1,$\frac{k({x}_{1}-4)}{{x}_{1}-2}$)
∴$\overrightarrow{AP}=(3,\frac{k({x}_{1}-4)}{{x}_{1}-2}),\overrightarrow{AN}=({x}_{2}+2,k({x}_{2}-4)$).
要证A,P,N三点共线,只证明$\overrightarrow{AP},\overrightarrow{AN}$共线即可,
即证明$\frac{k({x}_{1}-4)}{{x}_{1}-2}({x}_{2}+2)=3k({x}_{2}-4)$成立.
即证明2x1x2-5(x1+x2)-8=0,将①代入上式显然成立.
∴A,P,N三点共线.
(ii)将直线y=k(x-4)(k≠0)变形为x=my+4,(m=$\frac{1}{k}$).
联立$\left\{\begin{array}{l}{x=my+1}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$得(m2-4)y2+8my-12=0.△=16(m2-12)>0⇒m2>12.
|MN|=$\sqrt{1+{m}^{2}}\frac{4\sqrt{{m}^{2}-12}}{{m}^{2}+4}$,
点O到直线MN的距离d=$\frac{4}{\sqrt{1+{m}^{2}}}$.
△OMN面积S=$\frac{1}{2}$×|MN|×d=$\frac{8\sqrt{{m}^{2}-12}}{{m}^{2}+4}=\frac{8\sqrt{{m}^{2}-12}}{{m}^{2}-12+16}$=$\frac{8}{\sqrt{{m}^{2}-12}+\frac{16}{\sqrt{{m}^{2}-12}}}$$≤\frac{8}{8}=1$.
当且仅当m=±2$\sqrt{7}$,及k=±$\frac{\sqrt{7}}{14}$时等号成立.
∴当直线方程为:y=±$\frac{\sqrt{7}}{14}(x-4)$时,△OMN面积的最大为1.
点评 本题考查了椭圆的方程、直线与椭圆的位置关系、利用向量证明三点共线、运算能力,属于难题,


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
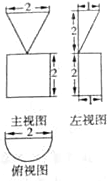
| A. | 2π | B. | $\frac{8}{3}$π | C. | $\frac{4}{3}$π | D. | $\frac{π}{3}$+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
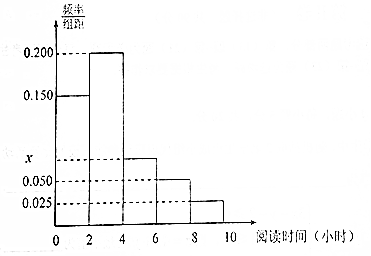 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 不喜欢戏剧 | 喜欢戏剧 | |
| 男性青年观众 | 40 | 10 |
| 女性青年观众 | 40 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com