
分析 (1)利用两角和差公式打开,根据同角三角函数关系式可求cosα的值;
(2)根据二倍角公式求出cos2α,sin2α,利用两角和差公式打开,可得sin(2α-$\frac{π}{4}$)的值.
解答 解:(1)sin(α+$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,
即sinαcos$\frac{π}{4}$+cosαsin$\frac{π}{4}$=$\frac{\sqrt{2}}{10}$,化简:sinα+cosα=$\frac{1}{5}$…①
sin2α+cos2α=1…②.
由①②解得cosα=-$\frac{3}{5}$或cosα=$\frac{4}{5}$
∵α∈($\frac{π}{2}$,π).
∴cosα=-$\frac{3}{5}$
(2)∵α∈($\frac{π}{2}$,π).cosα=-$\frac{3}{5}$
∴sinα=$\frac{4}{5}$,
那么:cos2α=1-2sin2α=$-\frac{7}{25}$,sin2α=2sinαcosα=$-\frac{24}{25}$
∴sin(2α-$\frac{π}{4}$)=sin2αcos$\frac{π}{4}$-cos2αsin$\frac{π}{4}$=$-\frac{17\sqrt{2}}{50}$.
点评 本题主要考查了两角和差公式,同角三角函数关系式以及二倍角公式的运用和计算能力.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,1) | B. | [-1,$\frac{1}{2}$] | C. | (-1,$\frac{1}{2}$] | D. | [-$\frac{1}{3}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
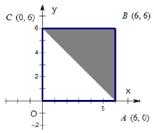 如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).
如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
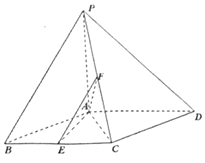 已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.
已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com