
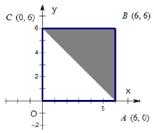
 如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).
如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界).分析 (Ⅰ)根据三角形和正方形的面积之比求出满足条件的概率即可;(Ⅱ)求出落在B内的可能,从而求出满足条件的概率即可.
解答 解:(Ⅰ)向区域A随机抛掷一枚黄豆,
黄豆落在区域B的概率$P=\frac{S_B}{S_A}=\frac{1}{2}$;
(Ⅱ)甲、乙两人各掷一次骰子,
占(x,y)共36种结可能.
其中落在B内的有26种可能,
即(1,5),(1,6),(2,4),(2,5),(2,6),
(3,3),(3,4),(3,5),(3,6),(4,2),
(4,3),(4,4),(4,5),(4,6),(5,1),
(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),
点(x,y)落在区B的概率p=$\frac{26}{36}$=$\frac{13}{18}$.
点评 本题考查了几何概型问题,考查列举法求概率问题,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,0,1,2,3} | C. | {1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 0 | C. | 2 | D. | $-\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
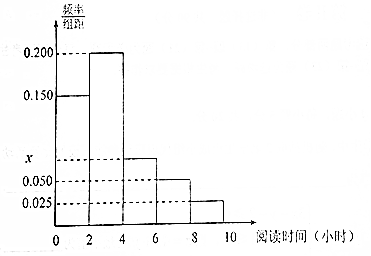 某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:
某学校为了了解本校高一学生每周课外阅读时间(单位:小时)的情况,按10%的比例对该校高一600名学生进行抽样统计,将样本数据分为5组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),并将所得数据绘制成如图所示的频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com