
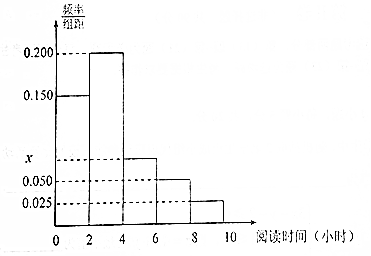
 ijѧУΪ���˽ⱾУ��һѧ��ÿ�ܿ����Ķ�ʱ�䣨��λ��Сʱ�����������10%�ı����Ը�У��һ600��ѧ�����г���ͳ�ƣ����������ݷ�Ϊ5�飺��һ��[0��2�����ڶ���[2��4����������[4��6����������[6��8����������[8��10���������������ݻ��Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
ijѧУΪ���˽ⱾУ��һѧ��ÿ�ܿ����Ķ�ʱ�䣨��λ��Сʱ�����������10%�ı����Ը�У��һ600��ѧ�����г���ͳ�ƣ����������ݷ�Ϊ5�飺��һ��[0��2�����ڶ���[2��4����������[4��6����������[6��8����������[8��10���������������ݻ��Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ������Ƶ�ʺ�Ϊ1���г��������x��ֵ��
��������Ƶ�ʷֲ�ֱ��ͼ����ƽ�������ɣ�
�������÷ֲ����ԭ������ӵ����顢�����顢�����������γ�ȡ��������
�ó�X�Ŀ���ȡֵ�������Ӧ�ĸ��ʣ�д���ֲ��У������ѧ������
��� �⣺������Ƶ�ʺ�Ϊ1���г�����
��0.150+0.200+x+0.050+0.025����2=1��
���x=0.075��
�����Ƹ�У��һѧ��ÿ�ܿ����Ķ���ƽ��ʱ��Ϊ
$\overline{x}$=1��0.3+3��0.4+5��0.15+7��0.1+9��0.05=3.40��Сʱ����
����������֪�ӵ����顢�����顢�����������ηֱ�
��ȡ3����2����1��ѧ�������X�Ŀ���ȡֵΪ0��1��2��
��P��X=0��=$\frac{{C}_{3}^{0}{•C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
P��X=1��=$\frac{{C}_{3}^{1}{•C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{3}{5}$��
P��X=2��=$\frac{{C}_{3}^{2}{•C}_{3}^{0}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
����X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ����ɢ����������ķֲ��С���ѧ�����ļ������⣬���ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
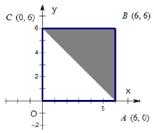 ��ͼ������A��������OABC�����߽磩������B��������ABC�����߽磩��
��ͼ������A��������OABC�����߽磩������B��������ABC�����߽磩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{2}$ | B�� | 4 | C�� | $\frac{9}{2}$ | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-3]��[2��+�ޣ� | B�� | ��-�ޣ�-3���ȣ�2��+�ޣ� | C�� | ��-3��2�� | D�� | [-3��2] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com