
分析 (Ⅰ)根据弦长公式即可求出p的值,问题得以解决,
(Ⅱ)联立方程组,根据韦达定理,即可求出过点A,B作抛物线E的切线l1,l2方程,再求出交点坐标,根据斜率的关系即可求出k的值.
解答 解:(Ⅰ)联立$\left\{\begin{array}{l}y=x+\frac{p}{2}\\{x^2}=2py\end{array}\right.$,消去x得${y^2}-3py+\frac{p^2}{4}=0$,
题设得$|AB|={y_A}+\frac{p}{2}+{y_B}+\frac{p}{2}={y_A}+{y_B}+p=4p=8$,
∴p=2,
∴抛物线E的方程为x2=4y.
(II)设$A({x_1},\frac{1}{2p}x_1^2),B({x_2},\frac{1}{2p}x_2^2)$
联立$\left\{\begin{array}{l}y=kx+\frac{p}{2}\\{x^2}=2py\end{array}\right.$,消去y得x2-2pkx-p2=0,
∴${x_1}+{x_2}=2pk,{x_1}•{x_2}=-{p^2}$,
由$y=\frac{1}{2p}{x^2}$得${y^'}=\frac{1}{p}x$,
∴直线l1,l2的方程分别为$y=\frac{x_1}{p}x-\frac{1}{2p}x_1^2,y=\frac{x_2}{p}x-\frac{1}{2p}x_2^2$,
联立$\left\{\begin{array}{l}y=\frac{x_1}{p}x-\frac{1}{2p}x_1^2\\ y=\frac{x_2}{p}x-\frac{1}{2p}x_2^2\end{array}\right.$得点P的坐标为$(pk,-\frac{p}{2})$,
∴${k_{PF}}=-\frac{1}{k}$,
∴$-\frac{1}{k}+k=-\frac{3}{2}∴k=-2$或$\frac{1}{2}$,
∴直线l的斜率为k=-2或 $k=\frac{1}{2}$.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,考查直线与抛物线的位置关系,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,1) | B. | [-1,$\frac{1}{2}$] | C. | (-1,$\frac{1}{2}$] | D. | [-$\frac{1}{3}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
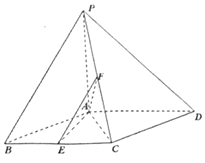 已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.
已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
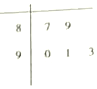 2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )
2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )| A. | 9 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com