
���� ��1�����������ε����ʿɵ�a=$\frac{3}{2}$�����ɵȲ����е����ʿɵ�a+c=4�����ɵõ�c�������õ����κ����Ľ���ʽ��
��2�����f��an+1����f��an����������֪�ĵ�ʽ�л���õ�����{$\frac{1}{{a}_{n}}$}Ϊ�Ȳ����У��������{$\frac{1}{{a}_{n}}$}��ͨ�ʽ���������{an}��ͨ�ʽ��
��3����bn=$\frac{1}{{a}_{n}}$�����cos��bn�У���Ȼ���nΪż���������������������{Sn•cos��bn�У�}��ǰn���Tn��
��� �⣺��1��a�DZ߳�Ϊ$\frac{3\sqrt{3}}{2}$���������ε����Բ�뾶��
�ɵ�a=$\frac{3\sqrt{3}}{2}$•$\frac{\sqrt{3}}{3}$=$\frac{3}{2}$��
��a��c�ĵȲ�������2���ɵ�a+c=4�����c=$\frac{5}{2}$��
��f��x��=$\frac{3}{2}$x2+x-$\frac{5}{2}$��
��2����f��an+1��-f��an��=$\frac{3}{2}$��an+1��2+��an+1��-$\frac{3}{2}$an2-an=3an+$\frac{5}{2}$��
��${a_1}=1��3{a_{n+1}}=1-\frac{1}{{f��{a_n}+1��-f��{a_n}��-\frac{3}{2}}}��n��{N^*}��$
=1-$\frac{1}{3{a}_{n}+1}$=$\frac{3{a}_{n}}{3{a}_{n}+1}$��
��$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$+3��
������{$\frac{1}{{a}_{n}}$}Ϊ����Ϊ1������Ϊ3�ĵȲ����У�
��$\frac{1}{{a}_{n}}$=1+3��n-1��=3n-2��
����an=$\frac{1}{3n-2}$��
��3����bn=3n-2��
��cos��bn�У�=cos��3n-2����=$\left\{\begin{array}{l}{-1��n=2k-1}\\{1��n=2k}\end{array}\right.$kΪ��������
��Sn•cos��bn�У�=��-1��nSn��
��Tn=-S1+S2-S3+S4-��+��-1��nSn��
�ٵ�nΪż��ʱ��Tn=��-S1+S2��+��-S3+S4��+��+��-Sn-1+Sn��
=b2+b4+��+bn=$\frac{3{n}^{2}+2n}{4}$��
�ڵ�nΪ����ʱ��
Tn=Tn-1-Sn=$\frac{3��n-1��^{2}+2��n-1��}{4}$-$\frac{n��3n-1��}{2}$=$\frac{-3{n}^{2}-2n+1}{4}$��
���ϣ�Tn=$\left\{\begin{array}{l}{\frac{-3{n}^{2}-2n+1}{4}��nΪ����}\\{\frac{3{n}^{2}+2n}{4}��nΪż��}\end{array}\right.$��
���� ���⿼���˶��κ����Ľ���ʽ���������˵Ȳ����е����ʺ����еĺ������ԣ����������еĵ���ʽ�����еĺͣ������˷������۵���ѧ˼�뷽����������ѧ���ۺϴ����ͽ�����������������һ���Ѷ���Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | -1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{n+2}{n}$ | B�� | $\frac{2n+1}{2n-1}$ | C�� | $-\frac{2n+1}{2n-1}$ | D�� | -$\frac{n+1}{n-1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
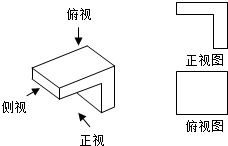 ����ͼ�У�ͼ��b����ͼ��a����ʵ�ﻭ��������ͼ����ͼ������Ϊ��ȷ�����������ȷ�����ҳ���������Ȼ������ͼ���ߴ粻���ϸ�Ҫ��
����ͼ�У�ͼ��b����ͼ��a����ʵ�ﻭ��������ͼ����ͼ������Ϊ��ȷ�����������ȷ�����ҳ���������Ȼ������ͼ���ߴ粻���ϸ�Ҫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com