
分析 (1)分a≤0、a>0两种情况,讨论f′(x)的正负即可;
(2)由题易得a=$\frac{{e}^{x}-\frac{1}{2}{x}^{2}-1}{x}$,利用零点的存在性定理,考查g(x)=$\frac{{e}^{x}-\frac{1}{2}{x}^{2}-1}{x}$ (x>0)在[1,2]上的单调性即可;
(3)通过变形,问题等价于证明$n(1-\frac{x}{n})^{n}{e}^{x}≥n-{x}^{2}$成立,通过(1)知${e}^{\frac{x}{n}}≥1+\frac{x}{n}$,利用$-\frac{{x}^{2}}{{n}^{2}}>-1$、及(1+x)n≥1+nx,化简即得$n(1-\frac{x}{n})^{n}{e}^{x}≥n-{x}^{2}$•
解答 解:(1)∵函数f(x)=ex-ax-1(a∈R),
∴f′(x)=ex-a,令f′(x)=0,解得x=lna,
当a≤0时,f′(x)≥0,则f(x)在(-∞,+∞)上单调递增,
当a>0时,f(x)在(-∞,lna)上单调递减,f(x)在(lna,+∞)上单调递增;
(2)∵F(x)=f(x)-$\frac{1}{2}$x2=0,∴a=$\frac{{e}^{x}-\frac{1}{2}{x}^{2}-1}{x}$,
考查g(x)=$\frac{{e}^{x}-\frac{1}{2}{x}^{2}-1}{x}$ (x>0),则g′(x)=$\frac{(x-1){e}^{x}-\frac{1}{2}{x}^{2}+1}{{x}^{2}}$,
令h(x)=$(x-1){e}^{x}-\frac{1}{2}{x}^{2}+1$,则h′(x)=x(ex-1),
当1≤x≤2时,h′(x)>0,则h(x)在[1,2]上单调递增,
∴h(x)≥h(1)=$\frac{1}{2}>$0,g′(x)>0,∴g(x)在[1,2]上单调递增,
∴g(x)=$\frac{{e}^{x}-\frac{1}{2}{x}^{2}-1}{x}$在[1,2]上的最小值为g(1)=e-$\frac{3}{2}$,
最大值为g(2)=$\frac{1}{2}({e}^{2}-3)$,
∴当$e-\frac{3}{2}≤a≤\frac{1}{2}({e}^{2}-3)$时,函数F(x)=f(x)-$\frac{1}{2}$x2在[1,2]上有且仅有一个零点;
(3)n-n(1-$\frac{x}{n}$)nex≤x2等价于$n(1-\frac{x}{n})^{n}{e}^{x}≥n-{x}^{2}$,
由(1)知ex≥1+x,∴${e}^{\frac{x}{n}}≥1+\frac{x}{n}$,
∵x2<n,且n∈N*,∴x2<n≤n2,∴$-\frac{{x}^{2}}{{n}^{2}}>-1$,
又∵(1+x)n≥1+nx,
∴n(1-$\frac{x}{n}$)nex=$n[(1-\frac{x}{n}){e}^{\frac{x}{n}}]^{n}$
≥$n[(1-\frac{x}{n})(1+\frac{x}{n})]^{n}$
=$n(1-\frac{{x}^{2}}{{n}^{2}})^{n}$
≥$n(1-n\frac{{x}^{2}}{{n}^{2}})$
=n-x2•
点评 本题考察了函数的单调性,导数的应用,不等式的证明,是一道综合题,注意解题方法的积累,属于难题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,点D在棱AA1上,且∠ACB=90°,AA1=BC=2,AC=1.
如图,直三棱柱ABC-A1B1C1中,点D在棱AA1上,且∠ACB=90°,AA1=BC=2,AC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
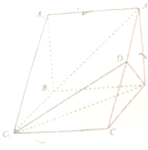 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com