
分析 (1)利用三角函数的化简求值,有理指数幂的运算法则化简求解即可.
(2)利用对数运算法则化简求解即可.
解答 解:(1)$\root{3}{(-4)^{3}}$-($\frac{1}{2}$)0+0.25${\;}^{\frac{1}{2}}$×($\frac{-1}{\sqrt{2}}$)-4-sin270°+tan15°
=-4-1+$\frac{1}{2}×{(\sqrt{2})}^{4}$+1+tan(45°-30°)
=-5+2+1+$\frac{tan45°+tan30°}{1-tan45°tan30°}$
=-2+2-$\sqrt{3}$=$-\sqrt{3}$ …..(6分)
(2)log3$\sqrt{27}$+lg25+2lg2+7${\;}^{3lo{g}_{7}2}$+$\frac{lg4+lg3}{1+\frac{1}{2}lg0.36+\frac{1}{3}lg8}$
=$\frac{3}{2}$+2+8+$\frac{lg12}{lg(10×0.6×2)}$=$\frac{3}{2}$+2+8+1=$\frac{25}{2}$…..(12分)
点评 本题考查三角函数的化简求值,有理指数幂以及对数运算法则的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {4} | C. | {1,3} | D. | {2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
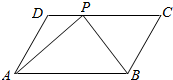
| A. | 18 | B. | 20 | C. | 22 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com