
分析 (Ⅰ)利用正弦定理将(2a+b)cosC+ccosB=0化简,可得角C的大小.c=6,利用余弦定理,构造基本不等式,即可求解△ABC面积的最大值.
解答 解:(Ⅰ)根据(2a+b)cosC+ccosB=0,由正弦定理可得:2sinAcosC+sinBcosC+sinCcosB=0.
即2sinAcosC=-sinA,
∵0<A<π,sinA≠0,
∴cosC=-$\frac{1}{2}$
∵0<C<π
∴C=$\frac{2π}{3}$.
(Ⅱ)∵c=6,C=$\frac{2π}{3}$.
由余弦定理:可得${c}^{2}={a}^{2}+{b}^{2}-2abcos\frac{2π}{3}$
即36=a2+b2+ab,
∵a2+b2≥2ab(当且仅当a=b时取等号)
∴3ab≤36,即ab≤12.
故得△ABC面积S=$\frac{1}{2}$absinC$≤\frac{1}{2}×12×\frac{\sqrt{3}}{2}=3\sqrt{3}$.
即△ABC面积的最大值为$3\sqrt{3}$.
点评 本题主要考查了正弦定理,余弦定理的化简计算能力,和基本不等式求最值的运用.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 命题“p∨q为真”是命题“p∧q为真”的必要条件 | |
| B. | 向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}•\overrightarrow{b}>0$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角 | |
| C. | 若am2≤bm2,则a≤b | |
| D. | “?x0∈R,x02-x0≤0”的否定是“?x∈R,x2-x≥0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
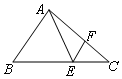 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )| A. | $\frac{{\sqrt{7}}}{14}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{14}$ | D. | $\frac{{\sqrt{21}}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 100 | 80 | 50 | 20 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 考核内容 | M(文化) | N(面试) | ||
| 得分 | 90 | 60 | 30 | 10 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 信心级别 | 非常有信心 | 有信心 | 不知道 | 没信心 |
| 信心指数(分数) | 90 | 60 | 30 | 6 |
| 人数(名) | 42 | 38 | 14 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{120}$ | B. | $\frac{7}{60}$ | C. | $\frac{7}{30}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com