
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
分析 在①中,由AA1$\underset{∥}{=}$EH$\underset{∥}{=}$GF,知四边形EFGH是平行四边形;在②中,平面α与平面BCC1B1平行或相交;在③中,EH⊥平面BCEF,从而平面α⊥平面BCFE.
解答 解: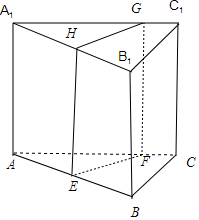 如图,∵在直三棱柱ABC-A1BlC1中,
如图,∵在直三棱柱ABC-A1BlC1中,
平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.
∴AA1$\underset{∥}{=}$EH$\underset{∥}{=}$GF,∴四边形EFGH是平行四边形,故①正确;
∵EF与BC不一定平行,∴平面α与平面BCC1B1平行或相交,故②错误;
∵AA1$\underset{∥}{=}$EH$\underset{∥}{=}$GF,且AA1⊥平面BCEF,∴EH⊥平面BCEF,
∵EH?平面α,∴平面α⊥平面BCFE,故③正确.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
| 甲 | 乙 | ||||||||||||
| 8 | 9 | 9 | 8 | 9 | 9 | 3 | 8 | 9 | 9 | ||||
| 2 | 0 | 1 | 0 | 4 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | ||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
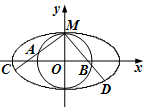 如图,圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)相切于点M(0,1).
如图,圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)相切于点M(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是奇函数 | |
| B. | f(x)是偶函数 | |
| C. | f(x)是周期函数 | |
| D. | f(x)在$[-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ](k∈z)$上为减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com