
���� ��1����x=-c������Բ���̿ɵã�${y}^{2}=\frac{{b}^{2}}{{a}^{2}}��{a}^{2}-{c}^{2}��$�����y���ɵ�|MN|=$\frac{2{b}^{2}}{a}$�����á�AMN�����$\frac{2+\sqrt{2}}{2}$=$\frac{1}{2}|MN||AF|$����Ϊ��2b2��a+c��=��2+$\sqrt{2}$a������$\frac{c}{a}=\frac{\sqrt{2}}{2}$��a2=b2+c2����������ɵó���
��2����P��-2��t����M��x1��y1����N��x2��y2�����߶�MN���е�Q��x0��y0����F��-1��0����ֱ��MN��б��Ϊ0ʱ�����������⣮��ֱ��MN�ķ���Ϊ��my=x+1��m=0ʱ��MN��x�ᣬ�ɵá�PMN���ǵȱ������Σ���ȥ��m��0ʱ������Բ����������Ϊ����m2+2��y2-2my-1=0�����ø���ϵ���Ĺ�ϵ�����е����깫ʽ������PQ��MN���ɵã�t��m2+2��=3m+2m3��������|PQ|=$\frac{\sqrt{3}}{2}$|MN|���ɵó���
��� �⣺��1����x=-c������Բ���̿ɵã�${y}^{2}=\frac{{b}^{2}}{{a}^{2}}��{a}^{2}-{c}^{2}��$�����y=$��\frac{{b}^{2}}{a}$����|MN|=$\frac{2{b}^{2}}{a}$�����AMN�����$\frac{2+\sqrt{2}}{2}$=$\frac{1}{2}|MN||AF|$=$\frac{1}{2}��\frac{2{b}^{2}}{a}$����a+c������Ϊ��2b2��a+c��=��2+$\sqrt{2}$a������$\frac{c}{a}=\frac{\sqrt{2}}{2}$��a2=b2+c2������ã�c=b=1��$a=\sqrt{2}$��
����Բ�ı�����Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}$=1��
��2����P��-2��t����M��x1��y1����N��x2��y2�����߶�MN���е�Q��x0��y0����F��-1��0����
ֱ��MN��б��Ϊ0ʱ�����������⣮
��ֱ��MN�ķ���Ϊ��my=x+1��
m=0ʱ��MN��x�ᣬ
|MN|=$\frac{2{b}^{2}}{a}$=$\sqrt{2}$����F��ֱ��x=-2�ľ���d=1����PMN���ǵȱ������Σ���ȥ��
m��0ʱ��
����$\left\{\begin{array}{l}{my=x+1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$��������m2+2��y2-2my-1=0��
��y1+y2=$\frac{2m}{{m}^{2}+2}$��y1y2=$\frac{-1}{{m}^{2}+2}$��
��y0=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{m}{{m}^{2}+2}$��x0=my0-1=$\frac{-2}{{m}^{2}+2}$��
��PQ��MN����$\frac{t-\frac{m}{{m}^{2}+2}}{-2+\frac{2}{{m}^{2}+2}}$��$\frac{1}{m}$=-1������t��m2+2��=3m+2m3��
|PQ|=$\frac{|-2-tm+1|}{\sqrt{1+{m}^{2}}}$=$\frac{|tm+1|}{\sqrt{1+{m}^{2}}}$��
|MN|=$\sqrt{��1+{m}^{2}��[��{y}_{1}+{y}_{2}��^{2}-4{y}_{1}{y}_{2}]}$=$\frac{2\sqrt{2}��1+{m}^{2}��}{2+{m}^{2}}$��
��|PQ|=$\frac{\sqrt{3}}{2}$|MN|����$\frac{|tm+1|}{\sqrt{1+{m}^{2}}}$=$\frac{\sqrt{3}}{2}$��$\frac{2\sqrt{2}��1+{m}^{2}��}{2+{m}^{2}}$��
������tm+1����2+m2��=$\sqrt{6}$��1+m2��$\sqrt{1+{m}^{2}}$��
��t��m2+2��=3m+2m3�����ɵã�m2=$\frac{1}{2}$�����m=$��\frac{\sqrt{2}}{2}$��
��ֱ��MN�ķ���Ϊ��$\sqrt{2}x$��y+$\sqrt{2}$=0��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ�ҳ����⡢һԪ���εĸ���ϵ���Ĺ�ϵ��б�ʼ��㹫ʽ���ȱ������ε����ʣ���������������������������������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Բ | B�� | ��Բ | C�� | ������ | D�� | ˫���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
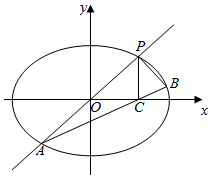 ��֪��Բw��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0�����㣨0��$\sqrt{2}$������Բw������һ�㵽������ľ���֮��Ϊ4��
��֪��Բw��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0�����㣨0��$\sqrt{2}$������Բw������һ�㵽������ľ���֮��Ϊ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | i��101�� | B�� | i��101�� | C�� | i��101�� | D�� | i��101�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com