
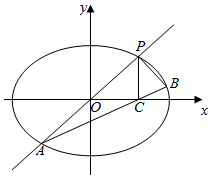
 已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.
已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.分析 (Ⅰ)利用已知条件列出方程,求出a,b即可求解椭圆W的方程.
(Ⅱ)①设P(x0,y0),则A(-x0,-y0),C(x0,0),推出${k_{\;}}=\;\frac{y_0}{x_0}$,然后求解直线AC的斜率.
②∠APB=90°,写出直线AB的方程:$y=\frac{k}{2}(x-{x_0})$,设点B(x1,y1),联立AB与椭圆方程,求出B的坐标,然后求解PB的斜率,利用直线垂直的充要条件证明即可.
解答 (本小题共14分)
解:(Ⅰ)由题意椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),可得:b=2,
∵2a=4,∴$a=2,b=\sqrt{2}$,-------------------(2分)
椭圆w的方程$\frac{x^2}{4}+\frac{y^2}{2}=1$.--------------------(4分)
(Ⅱ)①设P(x0,y0),则A(-x0,-y0),C(x0,0),${k_{\;}}=\;\frac{y_0}{x_0}$.--------------------(6分)
直线AB的斜率${k_1}=\;\frac{{0-(-{y_0})}}{{{x_0}-(-{x_0})}}=\frac{y_0}{{2{x_0}}}=\frac{k}{2}$.--------------------(7分)
②∠APB=90°--------------------(8分)
由①可得直线AB的方程:$y=\frac{k}{2}(x-{x_0})$,设点B(x1,y1
联立$\left\{\begin{array}{l}y=\frac{k}{2}(x-{x_0})\\{x^2}+2{y^2}=4\end{array}\right.$,
消去y得$(2+{k^2}){x^2}-2{k^2}{x_0}x+{k^2}{x_0}^2-8=0$-------------(10分)
则$-{x_0}+{x_1}=\frac{{2{k^2}{x_0}}}{{2+{k^2}}}$,解得${x_1}=\frac{{3{k^2}{x_0}+2{x_0}}}{{2+{k^2}}}$,------------(12分)
所以${y_1}=\frac{{{k^3}{x_0}}}{{2+{k^2}}}$,点$B(\frac{{3{k^2}{x_0}+2{x_0}}}{{2+{k^2}}},\frac{{{k^3}{x_0}}}{{2+{k^2}}})$.-----------(13分)
因为 ${k_{PB}}=\frac{{\frac{{{k^3}{x_0}}}{{2+{k^2}}}-k{x_0}}}{{\frac{{3{k^2}{x_0}+2{x_0}}}{{2+{k^2}}}-{x_0}}}=\frac{{-2k{x_0}}}{{2{k^2}{x_0}}}=-\frac{1}{k}$,
所以kAP•kPB=-1,所以∠APB=90°----------------------(14分)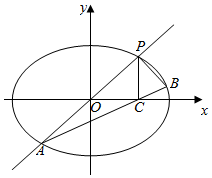
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
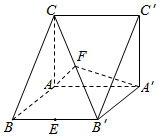 在三棱ABC-A′B′C′中,侧棱AA′⊥底面ABC,AC⊥AB,AB=2,AC=AA′=3,
在三棱ABC-A′B′C′中,侧棱AA′⊥底面ABC,AC⊥AB,AB=2,AC=AA′=3,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人数 课程 | 课程一 | 课程二 | 课程三 | 课程四 | 课程五 |
| 50 | + | + | - | + | - |
| 80 | + | + | - | - | - |
| 125 | + | - | + | - | + |
| 150 | - | + | + | + | - |
| 94 | + | - | - | + | + |
| 76 | - | - | + | + | - |
| 25 | - | - | + | - | + |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -240 | C. | -480 | D. | 960 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com