
| 人数 课程 | 课程一 | 课程二 | 课程三 | 课程四 | 课程五 |
| 50 | + | + | - | + | - |
| 80 | + | + | - | - | - |
| 125 | + | - | + | - | + |
| 150 | - | + | + | + | - |
| 94 | + | - | - | + | + |
| 76 | - | - | + | + | - |
| 25 | - | - | + | - | + |
分析 (1)根据图表求得既选课程三,又选了课程四的人数,与总人数的比值;
(2)观察图表查出选3项课程的总人数,与600的比值;
(3)分别求得选课程一、三和四的概率,进行比较,选出最大的概率.
解答 解:(1)学生既选了课程三,又选了课程四的概率为:$\frac{150+76}{600}$=$\frac{113}{300}$,
(2)学生在五项课程中,选了三项课程的概率为:$\frac{50+125+150+94}{600}$=$\frac{419}{600}$,
(3)某学生已经选了课程二,再选课程一的概率为:$\frac{50+80}{50+80+150}$=$\frac{13}{28}$;
再选课程三的概率为:$\frac{150}{50+80+150}$=$\frac{15}{28}$;
再选课程四的概率为:$\frac{50+150}{50+80+150}$=$\frac{5}{7}$;
所以,某学生已经选了课程二,那么该学生选择课程四的可能性最大.
点评 本题考查根据图表求概率,考查学生的观察能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
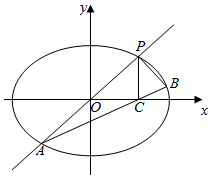 已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.
已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12}$,0)对称 | |
| B. | 可由函数f(x)的图象向右平移$\frac{π}{3}$个单位得到 | |
| C. | 可由函数f(x)的图象向左平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(x)的图象向左平移$\frac{π}{3}$个单位得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<2} | B. | {x|x<-1或1<x≤2} | C. | {x|x<-1} | D. | {x|x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
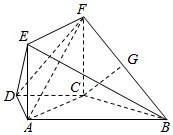 如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.
如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com