
分析 (1)由2Sn=4an+(n-4)(n+1),可求得a1,a2,a3的值,从而可猜想{an}的一个通项公式.
(2)按照数学归纳法的证题步骤:先证明n=1时命题成立,再假设当n=k时结论成立,去证明当n=k+1时,结论也成立,从而得出命题an=2n+n对任意的正整数n恒成立.
解答 解:(1)当n=1时,2S1=4a1-6,解得a1=3,
当n=2时,2(a1+a2)=4a2-6,解得a2=6,
当n=2时,2(a1+a2+a3)=4a3-4,解得a3=11,
由此猜想an=2n+n,(n∈N+).
下面用数学归纳法证明:an=2n+n,(n∈N+).
①当n=1时,显然成立,
②假设n=k时成立,即ak=2k+k,
那么当n=k+1时,
∵2ak+1=2Sk+1-2Sk=[4ak+1+(k-3)(k+2)]-[4ak+(k-4)(k+1),
∴ak+1=2ak-k+1=2×2k+2k-k+1=2k+1+k+1,
所以当n=k+1时,猜想成立,
由①②可知,猜想成立,即an=2n+n.(n∈N+).
点评 本题考查数学归纳法,考查推理证明的能力,假设n=k(k∈N*)时命题成立,去证明则当n=k+1时,用上归纳假设是关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
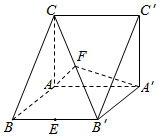 在三棱ABC-A′B′C′中,侧棱AA′⊥底面ABC,AC⊥AB,AB=2,AC=AA′=3,
在三棱ABC-A′B′C′中,侧棱AA′⊥底面ABC,AC⊥AB,AB=2,AC=AA′=3,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人数 课程 | 课程一 | 课程二 | 课程三 | 课程四 | 课程五 |
| 50 | + | + | - | + | - |
| 80 | + | + | - | - | - |
| 125 | + | - | + | - | + |
| 150 | - | + | + | + | - |
| 94 | + | - | - | + | + |
| 76 | - | - | + | + | - |
| 25 | - | - | + | - | + |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com