
分析 求两个曲线的交点,利用定积分的几何意义求区域面积.
解答 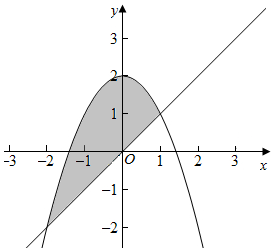 解:将y=x,代入y=2-x2得x=2-x2,解得x=-2或x=1,y=-2,y=1,
解:将y=x,代入y=2-x2得x=2-x2,解得x=-2或x=1,y=-2,y=1,
∴直线y=x和抛物线y=2-x2所围成封闭图形的面积如图所示,
∴S=${∫}_{-2}^{1}$(2-x-x2)dx=(2x-$\frac{1}{2}x$-$\frac{1}{3}{x}^{3}$)|${\;}_{-2}^{1}$=(2-$\frac{1}{3}$-$\frac{1}{2}$)-(-4+$\frac{8}{3}$-2)=$\frac{9}{2}$,
故答案为:$\frac{9}{2}$.
点评 本题主要考查积分的几何意义,联立曲线方程求出积分的上限和下限是解决本题的关键,比较基础.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
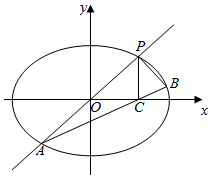 已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.
已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12}$,0)对称 | |
| B. | 可由函数f(x)的图象向右平移$\frac{π}{3}$个单位得到 | |
| C. | 可由函数f(x)的图象向左平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(x)的图象向左平移$\frac{π}{3}$个单位得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<2} | B. | {x|x<-1或1<x≤2} | C. | {x|x<-1} | D. | {x|x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | i<101? | B. | i>101? | C. | i≤101? | D. | i≥101? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com