

| A. | i<101? | B. | i>101? | C. | i≤101? | D. | i≥101? |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值.
解答 解:程序运行过程中,各变量值如下表所示:
第1次循环:S=0+1,i=1,
第2次循环:S=1+$\frac{1}{3}$,i=3,
第3次循环:S=1+$\frac{1}{3}$+$\frac{1}{5}$,i=5,…
依此类推,第51次循环:S=1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$,i=101,退出循环
其中判断框内应填入的条件是:i≤101,
故选:C.
点评 本题考查了当型循环结构的应用问题,解题时应准确理解流程图的含义,是基础题目.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{3}$,3) | C. | [1,3] | D. | [$\frac{1}{4}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
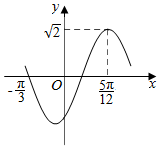 曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).
曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | (1,$\sqrt{5}$) | C. | ($\sqrt{3}$,+∞) | D. | ($\sqrt{5}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com