
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{3}$,3) | C. | [1,3] | D. | [$\frac{1}{4}$,1] |
分析 利用三角函数的诱导公式把已知函数化成正切函数,令$tan\frac{θ}{2}=t$(0<t<1),构造一个新函数g(t),再根据不等式的基本性质得到g(t)在(0,1)上必有最大值,然后求出m的取值范围.
解答 解:f(θ)=1+m+m($\frac{cosθ-1}{sinθ}$)+$\frac{sinθ-1}{cosθ}$=$1+m-mtan\frac{θ}{2}-\frac{1-tan\frac{θ}{2}}{1+tan\frac{θ}{2}}$,
令$tan\frac{θ}{2}=t$(0<t<1),则$g(t)=1+m-mt-\frac{1-t}{1+t}$=$2+2m-[m(t+1)+\frac{2}{t+1}]$,
$m(t+1)+\frac{2}{t+1}≥2\sqrt{2m}$当且仅当$m=\frac{2}{(t+1)^{2}}$时等号成立,即g(t)在(0,1)上必有最大值,
∴m的范围为($\frac{1}{2}$,2).
故选:A.
点评 本题考查三角函数的化简求值,考查不等式的基本性质,考查计算能力.是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12}$,0)对称 | |
| B. | 可由函数f(x)的图象向右平移$\frac{π}{3}$个单位得到 | |
| C. | 可由函数f(x)的图象向左平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(x)的图象向左平移$\frac{π}{3}$个单位得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<2} | B. | {x|x<-1或1<x≤2} | C. | {x|x<-1} | D. | {x|x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∩B=∅ | B. | A∩B=A | C. | A=B | D. | A∩B=B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | i<101? | B. | i>101? | C. | i≤101? | D. | i≥101? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
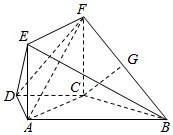 如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.
如图,在梯形ABCD中,AB∥CD,AB=2AD=2DC=2CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com