
分析 方法一:由图形的对称性质可得,方法二,S=${∫}_{\frac{π}{4}}^{π}$sinxdx-${∫}_{\frac{π}{4}}^{\frac{π}{2}}$cosxdx,分别根据定积分的定义即可求出.
解答 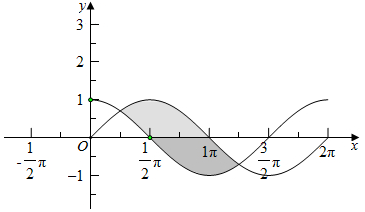 解:方法一:由图形的对称性质可得,$S=\frac{1}{2}\int_{\frac{π}{4}}^{\frac{5π}{4}}{(sinx-cosx)dx=\frac{1}{2}}(cos\frac{π}{4}+sin\frac{π}{4})-\frac{1}{2}(cos\frac{5π}{4}+sin\frac{5π}{4})=\sqrt{2}$.
解:方法一:由图形的对称性质可得,$S=\frac{1}{2}\int_{\frac{π}{4}}^{\frac{5π}{4}}{(sinx-cosx)dx=\frac{1}{2}}(cos\frac{π}{4}+sin\frac{π}{4})-\frac{1}{2}(cos\frac{5π}{4}+sin\frac{5π}{4})=\sqrt{2}$.
方法二:由图图可知,S=${∫}_{\frac{π}{4}}^{π}$sinxdx-${∫}_{\frac{π}{4}}^{\frac{π}{2}}$cosxdx=(1+$\frac{\sqrt{2}}{2}$)-(1-$\frac{\sqrt{2}}{2}$)=$\sqrt{2}$
故答案为:$\sqrt{2}$
点评 本题考查了定积分在几何中的应用,以及正弦余弦函数的图象,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{3}$,3) | C. | [1,3] | D. | [$\frac{1}{4}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
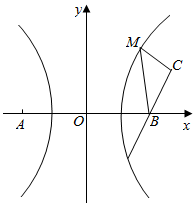 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )| A. | [$\sqrt{26}$+$\sqrt{2}$,+∞) | B. | [$\sqrt{26}$-$2\sqrt{2}$,+∞) | C. | [$\sqrt{26}$-$2\sqrt{2}$,$\sqrt{26}$+$2\sqrt{2}$) | D. | [$\sqrt{26}$-$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com