
| A. | A∩B=∅ | B. | A∩B=A | C. | A=B | D. | A∩B=B |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 降水量X | X<100 | 100≤X<200 | 200≤X<300 | X≥300 |
| 工期延误天数Y | 0 | 5 | 15 | 30 |
| 概率P | 0.4 | 0.2 | 0.1 | 0.3 |
| A. | 0.1 | B. | 0.3 | C. | 0.42 | D. | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{3}$,3) | C. | [1,3] | D. | [$\frac{1}{4}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0} | B. | {x|1≤x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x<或x≥2} |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
如图,抛物线 与
与 轴交于
轴交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,点
,点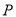 是
是 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点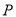 作
作 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点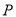 的横坐标为
的横坐标为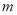 .
.
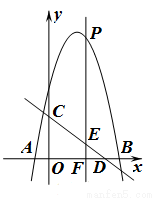
(1)求抛物线的解析式;
(2)若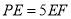 ,求
,求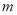 的值;
的值;
(3)若点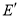 是点
是点 关于直线
关于直线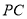 的对称点、是否存在点
的对称点、是否存在点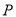 ,使点
,使点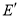 落在
落在 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点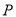 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com