
【题目】已知函数![]() 的图像与直线
的图像与直线![]() 相切.
相切.
(Ⅰ)求![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,设
,设![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
【答案】(Ⅰ) ![]() ,函数的单调减区间为
,函数的单调减区间为![]() ,增区间为
,增区间为![]() ; (Ⅱ)答案见解析.
; (Ⅱ)答案见解析.
【解析】试题分析:
(Ⅰ)由题意结合导函数与原函数切线的关系得到关于实数m的方程,解方程可得m=1,则函数的单调减区间为![]() ,增区间为
,增区间为![]() ;
;
(Ⅱ)原问题转化为函数![]() 的图象的交点个数,分类讨论可得:
的图象的交点个数,分类讨论可得:
当![]() 时,函数
时,函数![]() 无零点;
无零点;
当![]() 或
或![]() 时,函数
时,函数![]() 恰有一个零点;
恰有一个零点;
当![]() 时,函数
时,函数![]() 恰有两个零点.
恰有两个零点.
试题解析:
(I)设![]() 的图像与直线
的图像与直线![]() 相切于点
相切于点![]() ,
,
![]() ,
, ![]()
则 即
即
解得:![]()
由![]() 得
得![]() ;
;![]() 得
得![]() ;
;
所以函数![]() 的单调减区间为
的单调减区间为![]() ;增区间为
;增区间为![]()
(II)![]()
![]()
![]() ;
;
![]()
记函数![]()
![]()
由![]() 得
得![]() ;
;![]() 得
得![]()
![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
![]()
又![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;且
;且![]() .
.
则:当![]() 时,
时, ![]() 与
与![]() 的图像无交点,函数
的图像无交点,函数![]() 无零点;
无零点;
当![]() 或
或![]() 时,
时, ![]() 与
与![]() 的图像恰有一个交点,函数
的图像恰有一个交点,函数![]() 恰有一个零点;
恰有一个零点;
当![]() 时,
时, ![]() 与
与![]() 的图像恰有两个交点,函数
的图像恰有两个交点,函数![]() 恰有两个零点.
恰有两个零点.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且bsinA=asin2B.
(Ⅰ)求角B;
(Ⅱ)若b= ![]() ,a+c=ac,求△ABC的面积.
,a+c=ac,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx+![]() ax2+x+1.
ax2+x+1.
(I)a=﹣2时,求函数f(x)的极值点;
(Ⅱ)当a=0时,证明xex≥f(x)在(0,+∞)上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从盛满2升纯酒精的容器里倒出1升,然后加满水,再倒出1升混合溶液后又用水填满,以此继续下去,则至少应倒次后才能使纯酒精体积与总溶液的体积之比低于10%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
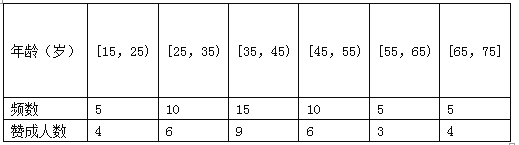
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
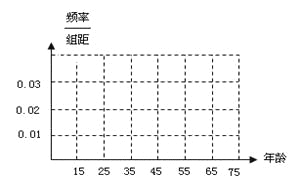
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
(l)计算这40名广场舞者中年龄分布在![]() 的人数;
的人数;
(2)若从年龄在![]() 中的广场舞者任取2名,求这两名广场舞者中恰有一人年龄在
中的广场舞者任取2名,求这两名广场舞者中恰有一人年龄在![]() 的概率.
的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的导数y′=f′(x)仍是x的函数,就把y′=f′(x)的导数y″=f″(x)叫做函数y=f(x)二阶导数,记做y(2)=f(2)(x).同样函数y=f(x)的n﹣1阶导数的导数叫做y=f(x)的n阶导数,表示y(n)=f(n)(x).在求y=ln(x+1)的n阶导数时,已求得 ![]() ,
, ![]() ,根据以上推理,函数y=ln(x+1)的第n阶导数为 .
,根据以上推理,函数y=ln(x+1)的第n阶导数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com