
| A. | 6 | B. | 3$\sqrt{3}$ | C. | 4 | D. | 5 |
分析 由题意可知设l2:y=t,设P(-1,t),(t∈R),M(x,y),则y=t,且|MP|=|MF2|,(x+1)2=(x-1)2+y2,化简可得:曲线C2:y2=4x,根据抛物线的定义可知:,当A,Q,Q′三点共线时,|QA|+|QQ′丨取最小值,即可求得|QA|+|QB|的最小值.
解答 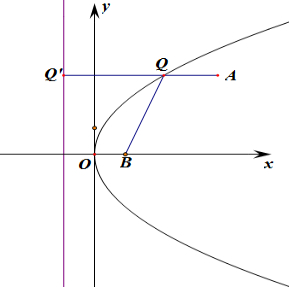 解:∵圆C:$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1的左右焦点为F1,F2,
解:∵圆C:$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1的左右焦点为F1,F2,
∴F1(-1,0),F2(1,0),直线l1:x=-1,
设l2:y=t,设P(-1,t),(t∈R),M(x,y),
则y=t,且|MP|=|MF2|,
∴(x+1)2=(x-1)2+y2,
∴曲线C2:y2=4x,
则B(1,0)为曲线C2:y2=4x焦点,
过Q做QQ′垂直于曲线C2的准线,
由抛物线的定义可知:丨QQ′丨=丨QB丨,
|QA|+|QB|=|QA|+|QQ′丨,当A,Q,Q′三点共线时,|QA|+|QQ′丨取最小值,
则Q′(-1,3),则|QA|+|QQ′丨的最小值为4-(-1)=5,
∴|QA|+|QB|的最小值5,
故选D.
点评 本题考查椭圆的标准方程,曲线轨迹方程的求法,抛物线的定义,考查数形结合思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
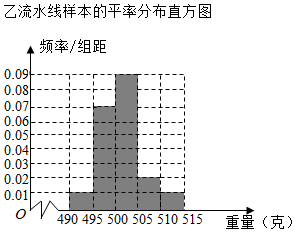 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品,统计结果如表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品,统计结果如表:| 产品重量(克) | 频数 |
| [490,495) | 6 |
| [495,500) | 8 |
| [500,505) | 14 |
| [505,510) | 8 |
| [510,515] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30o | B. | 60o | C. | 120o | D. | 150o |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,5} | B. | {2,4,6} | C. | {1,5} | D. | {1,6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com