
分析 求出f(x)的导数和极值,以及区间端点处的函数值,比较可得最值,即可得到|f(x1)-f(x2)|的最大值,进而得到t的范围,可得所求最小值.
解答 解:函数f(x)=x3-3x的导数为f′(x)=3x2-3,
令f′(x)=0,解得x=±1,
所以1,-1为函数f(x)的极值点.
因为f(-3)=-18,f(-1)=2,f(1)=-2,f(2)=2,
所以在区间[-3,2]上,f(x)max=2,f(x)min=-18,
所以对于区间[-3,2]上任意的x1,x2,|f(x1)-f(x2)|≤20,
所以t≥20,从而t的最小值为20.
故答案为:20.
点评 本题考查函数的最值的求法,注意运用导数,求极值和区间端点处的函数值,考查转化思想和运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\frac{3}{2}$ | C. | 0 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3$\sqrt{3}$ | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 该命题是真命题 | |
| B. | 该命题是假命题,因为大前提是错误的 | |
| C. | 该命题是假命题,因为小前提是错误的 | |
| D. | 该命题是假命题,因为结论是错误的 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
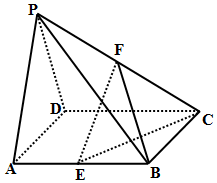 如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com