
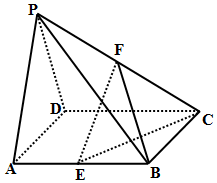
 如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.分析 (1)取PD中点G,连结GF、AG,由三角形中位线定理可得GF∥CD且$GF=\frac{1}{2}CD$,再由已知可得AE∥CD且$AE=\frac{1}{2}CD$,从而得到EFGA是平行四边形,则EF∥AG,然后利用线面平行的判定可得EF∥面PAD;
(2)取AD中点O,连结PO,由面面垂直的性质可得PO⊥面ABCD,且$PO=\sqrt{3}$,求出F到面ABCD距离$d=\frac{PO}{2}=\frac{{\sqrt{3}}}{2}$,然后利用等积法求得三棱锥B-EFC的体积;
(3)连OB交CE于M,可得Rt△EBC≌Rt△OAB,得到OM⊥EC.进一步证得PM⊥EC,可得∠PMO是二面角P-EC-D的平面角,然后求解直角三角形可得二面角P-EC-D的正切值.
解答 (1)证明:取PD中点G,连结GF、AG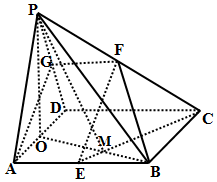 ,
,
∵GF为△PDC的中位线,∴GF∥CD且$GF=\frac{1}{2}CD$,
又AE∥CD且$AE=\frac{1}{2}CD$,∴GF∥AE且GF=AE,
∴EFGA是平行四边形,则EF∥AG,
又EF?面PAD,AG?面PAD,
∴EF∥面PAD;
(2)解:取AD中点O,连结PO,
∵面PAD⊥面ABCD,△PAD为正三角形,∴PO⊥面ABCD,且$PO=\sqrt{3}$,
又PC为面ABCD斜线,F为PC中点,∴F到面ABCD距离$d=\frac{PO}{2}=\frac{{\sqrt{3}}}{2}$,
故${V_{B-EFC}}={V_{F-BCE}}=\frac{1}{3}×\frac{1}{2}×1×2×\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{6}$;
(3)解:连OB交CE于M,可得Rt△EBC≌Rt△OAB,
∴∠MEB=∠AOB,则∠MEB+∠MBE=90°,即OM⊥EC.
连PM,又由(2)知PO⊥EC,可得EC⊥平面POM,则PM⊥EC,
即∠PMO是二面角P-EC-D的平面角,
在Rt△EBC中,$BM=\frac{BE•BC}{CE}=\frac{{2\sqrt{5}}}{5}$,∴$OM=OB-BM=\frac{{3\sqrt{5}}}{5}$,
∴$tan∠PMO=\frac{PO}{OM}=\frac{{\sqrt{15}}}{3}$,即二面角P-EC-D的正切值为$\frac{{\sqrt{15}}}{3}$.
点评 本题考查线面平行的判定,考查二面角的平面角及其求法,训练了利用等积法求多面体的体积,是中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac>bc | B. | 若a2>b2,则a>b>0 | ||
| C. | 若|x-3|>1,则2<x<4 | D. | 若|x2-3|>1,则$\sqrt{2}<x<2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
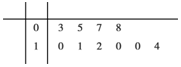 学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下:
学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com