考点:数列与不等式的综合,等比关系的确定,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)由已知3tS
n-(2t+3)S
n-1=3t,可得3ts
n-1-(2t+3)s
n-2=3t,两式相减可得数列a
n与a
n-1的递推关系,从而可证.
(2)由(1)可得f(t),代入整理可得b
n-b
n-1=
,利用等差数列的通项公式可求.
(3)把所求式两项结合,分组求和,即可得出结论.
解答:
(1)证明:∵3ts
n-(2t+3)s
n-1=3t∴3ts
n-1-(2t+3)s
n-2=3t(n>2)
两式相减可得3t(s
n-s
n-1)-(2t+3)(s
n-1-s
n-2)=0
整理可得3ta
n=(2t+3)a
n-1(n≥3)
∴
=
,
∵a
1=1,∴a
2=
,
∴
=
∴数列{a
n}是以1为首项,以
为公比的等比数列;
(2)解:由(1)可得f(t)=
.
在数列{b
n}中,b
n=f(
)=
=b
n-1+
,
∴b
n-b
n-1=
∴数列{b
n}以1为首项,以
为公差的等差数列
∴b
n=1+(n-1)×
=
n+
;
(3)证明:T
n=b
1b
2-b
2b
3+b
3b
4-b
4b
5+…-b
2nb
2n+1=b
2(b
1-b
3)+b
4(b
3-b
5)+…+b
2n(b
2n-1-b
2n+1)
=-
(b
2+b
4+…+b
2n)=-
(
n2+n)≤-
.
点评:本题主要考查了利用递推关系实现数列和与项的相互转化,进而求通项公式,等差数列的通项公式的运用,数列的求和.



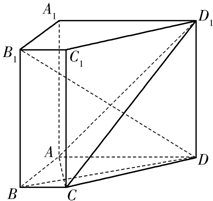 如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.
如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.