
分析 不等式ax2+x-1<0对任意x∈[1,3]成立转化为a<$\frac{1}{{x}^{2}}$-$\frac{1}{x}$,求出f(t)=t2-t,t=$\frac{1}{x}$∈[$\frac{1}{3}$,1]的最小值即可.
解答 解:不等式ax2+x-1<0对任意x∈[1,3]成立,
∴ax2<1-x,
即a<$\frac{1}{{x}^{2}}$-$\frac{1}{x}$;
设f(t)=t2-t,t=$\frac{1}{x}$∈[$\frac{1}{3}$,1];
∴f(t)=${(t-\frac{1}{2})}^{2}$-$\frac{1}{4}$,
当t=$\frac{1}{2}$时,f(t)取得最小值-$\frac{1}{4}$;
∴a<-$\frac{1}{4}$,
即a的范围是(-∞,-$\frac{1}{4}$).
故答案为:(-∞,-$\frac{1}{4}$).
点评 本题考查了函数的性质与应用问题,也考查了不等式应用问题,是基础题目


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
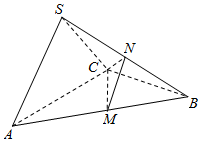 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M、N分别为AB,SB的中点.
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M、N分别为AB,SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
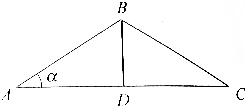 如图,屋顶的断面图是等腰三角形ABC,其中AB=BC,横梁AC的长为定值2l,试问:当屋顶面的倾斜角α为多大时,雨水从屋顶(顶面为光滑斜面)上流下所需A的时间最短?
如图,屋顶的断面图是等腰三角形ABC,其中AB=BC,横梁AC的长为定值2l,试问:当屋顶面的倾斜角α为多大时,雨水从屋顶(顶面为光滑斜面)上流下所需A的时间最短?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com