
分析 (1)求出导数,讨论x>0,x<0,导数的符号,注意运用指数函数的单调性,求出单调区间;
(2)当x∈[-2,2]时,不等式f(x)>m恒成立,即为当x∈[-2,2]时,f(x)min>m,由(1)即可求出最小值.
解答 解:(1)∵函数f(x)=$\frac{1}{2}$x2+ex-xex.
∴f(x)的定义域为R,
f'(x)=x+ex-(ex+xex)=x(1-ex),
当x<0时,1-ex>0,f'(x)<0;当x>0时,1-ex<0,f'(x)<0
∴f(x)在R上为减函数,
即f(x)的单调递减区间为(-∞,+∞).
(2)当x∈[-2,2]时,不等式f(x)>m恒成立,
即为当x∈[-2,2]时,f(x)min>m.
由(1)可知,f(x)在[-2,2]上单调递减,
∴f(x)min=f(2)=2-e2,
∴m<2-e2时,不等式f(x)>m恒成立.
点评 本题考查导数的综合应用:求单调区间、求最值,考查不等式恒成立问题转化为求函数的最值问题,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{4}{3}$] | B. | [3,+∞) | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
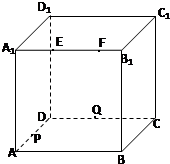 如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:
如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{|x|}{x}$是奇函数 | B. | f(x)=x2,x∈(-3,3]是偶函数 | ||
| C. | f(x)=(x-3)2是非奇非偶函数 | D. | y=x4+x2是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
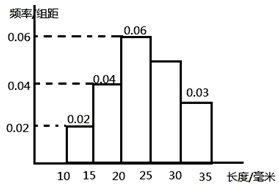 对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;
对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com