Question

6．给出下列命题：①若$\overrightarrow{a}$，$\overrightarrow{b}$共线，且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则（$\overrightarrow{a}-\overrightarrow{b}$）∥（$\overrightarrow{a}$+$\overrightarrow{b}$）；②已知$\overrightarrow{a}$=2$\overrightarrow{e}$，$\overrightarrow{b}$=3$\overrightarrow{e}$，则$\overrightarrow{a}$=$\frac{3}{2}$$\overrightarrow{b}$；③若$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=-3$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$，且$\overrightarrow{{e}_{1}}$≠$\overrightarrow{{e}_{2}}$，则|$\overrightarrow{a}$|=3|$\overrightarrow{b}$|；④△ABC中，AD是BC边上的中线，则$\overline{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AD}$，其中正确的序号是①③④．

Answer 1

分析 ①根据题意得出$\overrightarrow{a}$与$\overrightarrow{b}$是相等向量或相反向量，判断（$\overrightarrow{a}-\overrightarrow{b}$）∥（$\overrightarrow{a}$+$\overrightarrow{b}$）正确；
②又平面向量的线性运算，得出$\overrightarrow{a}$与$\overrightarrow{b}$数量关系；
③根据题意得出$\overrightarrow{b}$=-3$\overrightarrow{a}$，即得|$\overrightarrow{a}$|=3|$\overrightarrow{b}$|；
④画出图形，结合图形，得出$\overline{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AD}$正确．

解答 解：对于①，当$\overrightarrow{a}$，$\overrightarrow{b}$共线，且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|时，$\overrightarrow{a}$与$\overrightarrow{b}$是相等向量或相反向量，
∴（$\overrightarrow{a}-\overrightarrow{b}$）∥（$\overrightarrow{a}$+$\overrightarrow{b}$），①正确；
对于②，∵$\overrightarrow{a}$=2$\overrightarrow{e}$，$\overrightarrow{b}$=3$\overrightarrow{e}$，∴$\frac{1}{2}$$\overrightarrow{a}$=$\frac{1}{3}$$\overrightarrow{b}$，∴$\overrightarrow{a}$=$\frac{2}{3}$$\overrightarrow{b}$，②错误；
对于③，∵$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$，∴$\overrightarrow{b}$=-3$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$=-3（$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$）=-3$\overrightarrow{a}$，
又$\overrightarrow{{e}_{1}}$≠$\overrightarrow{{e}_{2}}$，∴|$\overrightarrow{a}$|=3|$\overrightarrow{b}$|，③正确；
对于④，△ABC中，AD是BC边上的中线，如图所示，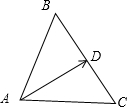

∴$\overline{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AD}$，④正确．
综上，以上正确的命题序号是①③④．
故答案为：①③④．

点评 本题考查了平面向量的线性运算与几何意义的应用问题，是基础题目．