
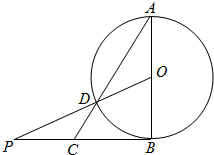
 如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.
如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$. 分析 连接BD,证明△PCD∽△PDB,求出PC,即可求出BC
解答 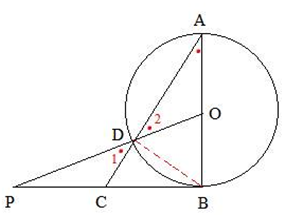 解:如图所示,连接BD,
解:如图所示,连接BD,
∵AB为⊙O的直径,
∴OA=OB=OD=$\frac{1}{2}$AB=1,
∵PB是⊙O的切线,
∴AB⊥PB,∠A=∠PBD,
∴OP=$\sqrt{O{B}^{2}+P{B}^{2}}$=3,
∴PD=OP-OD=2,
∵OA=OD,
∴∠A=∠2=∠1,
∴∠1=∠PBD,
∵∠P=∠P,
∴△PCD∽△PDB,
∴$\frac{PD}{PB}$=$\frac{PC}{PD}$,
∴PC=$\frac{P{D}^{2}}{PB}$=$\sqrt{2}$,
∴BC=PB-PC=$\sqrt{2}$,
故答案为:$\sqrt{2}$
点评 本题考查与圆有关的比例线段,考查三角形相似的证明,比较基础.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点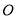 为极点,
为极点,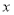 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为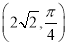 ,曲线
,曲线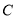 的参数方程为
的参数方程为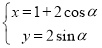 (
(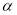 为参数).
为参数).
(1)直线 过
过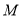 且与曲线
且与曲线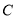 相切,求直线
相切,求直线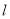 的极坐标方程;
的极坐标方程;
(2)点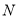 与点
与点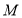 关于
关于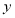 轴对称,求曲线
轴对称,求曲线 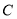 上的点到点
上的点到点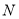 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com