
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
分析 先由$\overrightarrow{FB}$=2$\overrightarrow{FA}$,得出A为线段FB的中点,再借助于图象分析出其中一条渐近线对应的倾斜角的度数,找到a,b之间的等量关系,进而求出双曲线的离心率.
解答 解:如图过F作双曲线C的一条渐近线的垂线,垂足为A,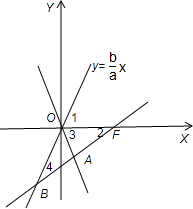
延长FA与另一条渐近线交于点B.所以FB⊥OA,
又因为$\overrightarrow{FB}$=2$\overrightarrow{FA}$,所以A为线段FB的中点,
∴∠2=∠4,又∠1=∠3,∠2+∠3=90°,
所以∠1=∠2+∠4=2∠2=∠3.
故∠2+∠3=90°=3∠2⇒∠2=30°⇒∠1=60°⇒$\frac{b}{a}$=$\sqrt{3}$.
∴$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}$=3,e2=$\frac{{c}^{2}}{{a}^{2}}$=4⇒e=2.
故选A.
点评 本题是对双曲线的渐近线以及离心率的综合考查,同时考查平面向量的共线定理的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | $\sqrt{7}$ | D. | $\frac{{\sqrt{21}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.
点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
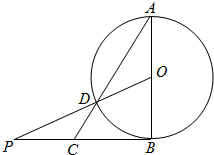 如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.
如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )| A. | 点P到平面QEF的距离 | B. | 三棱锥P-QEF的体积 | ||
| C. | 直线PQ与平面PEF所成的角 | D. | 二面角P-EF-Q的大小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com