
分析 (1)直线l为抛物线y=2x2的准线,F为其焦点,PN⊥l,AN1⊥l,由抛物线的定义知,|PF|=|PN|,可得|AP|+|PF|=|AP|+|PN|≥|AN1|,当且仅当A、P、N三点共线时取等号.
(2)建立如图所示的坐标系,设抛物线方程x2=-2py,抛物线过点(26,-6.5),代入抛物线方程求出参数p 即得抛物线方程;把y=-0.5代入抛物线的方程求得|x|值,由此值与5比较,可知竹排能安全通过此桥.
解答  解:(1)如图所示,直线l为抛物线y=2x2的准线,F为其焦点,PN⊥l,AN1⊥l,
解:(1)如图所示,直线l为抛物线y=2x2的准线,F为其焦点,PN⊥l,AN1⊥l,
由抛物线的定义知,|PF|=|PN|,
∴|AP|+|PF|=|AP|+|PN|≥|AN1|,当且仅当A、P、N三点共线时取等号.∴P点的横坐标与A点的横坐标相同即为1,
∴P(1,2);
(2)建立坐标系,设抛物线解析式为x2=-2py(p>0)
把(26,-6.5)代入,
解得抛物线:x2=-104y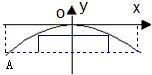
当y=6-6.5=-0.5时,x=±2$\sqrt{13}$,则有4$\sqrt{13}$>4,所以木箱能安全通过.
点评 本题考查了抛物线的定义、标准方程及其性质、最小值问题,考查用待定系数法求抛物线的标准方程的方法,以及利用抛物线的方程解决实际问题.属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
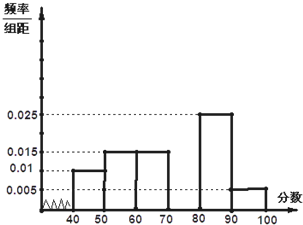 某学校从参加高一年级期末考试的学生中抽出20名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
某学校从参加高一年级期末考试的学生中抽出20名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (0,1) | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | a>b>c | C. | a>c>b | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com