
分析 (1)利用平面向量垂直的性质,正弦定理,三角形内角和定理可得2sinAcosB+sinA=0,结合sinA≠0,可求cosB,即可得解B的值.
(2)由余弦定理可求ac的值,利用三角形面积公式即可计算得解.
解答 (本题满分为12分)
解:(1)由向量$\overrightarrow{m}$=(cosB,cosC),$\overrightarrow{n}$=(2a+c,b),且$\overrightarrow{m}$⊥$\overrightarrow{n}$,
得(2a+c)cosB+bcosC=0,
得2sinAcosB+sinA=0,由于sinA≠0,可得:cosB=-$\frac{1}{2}$,
可得:B=$\frac{2π}{3}$…6分
(2)由b=2,a+c=3,B=$\frac{2π}{3}$,
∴22=a2+c2-2accosB=(a+c)2-ac,
∴可得:ac=5,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{5\sqrt{3}}{4}$…12分
点评 本题主要考查了平面向量垂直的性质,正弦定理,三角形内角和定理,余弦定理,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:解答题
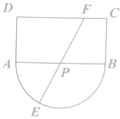 如城某观光区的平面示意图如图所示,其中矩形ABCD的长AB=2千米,宽AD=1千米,半圆的圆心P为AB中点,为了便于游客观光休闲,在观光区铺设一条由圆弧$\widehat{AE}$、线段EF、FC组成的观光道路,其中线段EF经过圆心P,且点F在线段CD上(不含线段端点C,D),已知道路AE,FC的造价为2a(a>0)元每千米,道路EF造价为7a元每千米,设∠APE=θ,观光道路的总造价为y.
如城某观光区的平面示意图如图所示,其中矩形ABCD的长AB=2千米,宽AD=1千米,半圆的圆心P为AB中点,为了便于游客观光休闲,在观光区铺设一条由圆弧$\widehat{AE}$、线段EF、FC组成的观光道路,其中线段EF经过圆心P,且点F在线段CD上(不含线段端点C,D),已知道路AE,FC的造价为2a(a>0)元每千米,道路EF造价为7a元每千米,设∠APE=θ,观光道路的总造价为y.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0) | B. | [-1,0)∪(0,+∞) | C. | (0,+∞) | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com