
分析 根据题意可得:an+2等于anan+1的个位数,所以可得a3=2,a4=4,a5=8,a6=2,a7=6,a8=2,a9=2,a10=4,进而得到数列的一个周期为6,求出两个周期的和,推出周期的数目,即可得到答案.
解答 解:由题意得,a3=a1•a2=2,由题意可得:a4=4,
依此类推,a5=8,a6=2,a7=6,a8=2,a9=2,a10=4,
可以根据以上的规律看出数列除第一项外是一个周期为6的周期数列,
一个周期的数值的和为:2+2+4+8+2+6=24,
因为243=24×10+3,
就是说,数列有10个周期加上第一项1以及2这一项,
所以数列共有:1+10×6+1=62.
故答案为:62
点评 本题是中档题,考查周期数列的求法,注意周期数列的首项与项数,数列的前n项和,考查形式分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
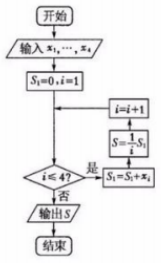 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为xi(i=1,2,3,4)(单位:立方米).根据如图所示的程序框图,若知x1,x2,x3,x4分别为1,1.5,1.5,3,则输出的结果S为$\frac{7}{4}$.
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为xi(i=1,2,3,4)(单位:立方米).根据如图所示的程序框图,若知x1,x2,x3,x4分别为1,1.5,1.5,3,则输出的结果S为$\frac{7}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 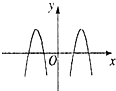 | B. | 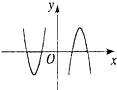 | C. | 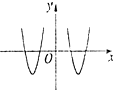 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com