
已知椭圆C:  +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为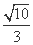 时,求k的值.
时,求k的值.
科目:高中数学 来源: 题型:
已知定义域为R的函数f(x)既是奇函数,又是周期为3的周期函数,
当x∈(0, )时,f(x)=sin πx,f
)时,f(x)=sin πx,f =0,则函数f(x)在区间[0,6]上的零点个数是( )
=0,则函数f(x)在区间[0,6]上的零点个数是( )
(A)3 (B)5 (C)7 (D)9
查看答案和解析>>
科目:高中数学 来源: 题型:
已知F是双曲线C: 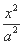 -
-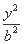 =1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且
=1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且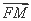 =2
=2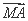 ,则双曲线C离心率是 .
,则双曲线C离心率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C:  +
+ =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF= ,则C的离心率为( )
,则C的离心率为( )
(A)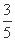 (B)
(B)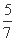 (C)
(C) (D)
(D)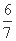
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆Γ:  +
+ =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y= (x+c)与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 .
(x+c)与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知左焦点为F(-1,0)的椭圆过点E(1,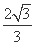 ).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
(1)求椭圆的标准方程;
(2)若P为线段AB的中点,求k1;
(3)若k1+k2=1,求证直线MN恒过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C1:  +
+ =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
(1)求椭圆C1的方程;
(2)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.当线段AP的中点与MN的中点的横坐标相等时,求h的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人调查身体状况,则应怎样抽样?
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
(3)若要抽20人调查对2016年巴黎奥运会筹备情况的了解,则应怎样抽样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com