
| A. | x1<x2<x3<x4 | B. | x3<x1<x4<x2 | C. | x1<x3<x4<x2 | D. | x1<x3<x2<x4 |
分析 由题意把两根是x1,x2代入方程求出f(x),设t=(x-x1)(x-x2)代入f(x),化简f(f(x))-x后求出f(f(x))=x,利用条件和韦达定理得x3+x4=x1+x2-2,根据不等式的性质和作差法分别判断出四个根的大小关系.
解答 解:由题意知,f(x)-x=0的两根是x1,x2,
则f(x)-x=(x-x1)(x-x2),即f(x)=x+(x-x1)(x-x2),
t=(x-x1)(x-x2),则f(x)=x+t,
所以f(f(x))-x=f(x)+[f(x)-x1][f(x)-x2]-x
=x+t+(x-x1+t)(x-x2+t)-x
=t2+(2x-x1-x2+2)t
由f(f(x))-x=0得,t=0或t+2x-x1-x2+2=0,
所以(x-x1)(x-x2)+2x-x1-x2+2=0,
则x2-(x1+x2-2)x+x1x2-(x1+x2-2)=0,
所以x3、x4是上述方程的解,则x3+x4=x1+x2-2,
因为x2-x1>2,所以x2>x1,x1<x2+2,
又x3<x4,所以2x3<x3+x4=x1+x2-2<2x2,则x3<x2,
同理可得,2x4>x3+x4=x1+x2-2>2x1,则x4>x1,
因为x2-x4>x3-x4,x3-x4<0,所以x2>x4,
同理可得,x1-x3>x4-x3,x4-x3>0,所以x1>x3,
所以x2>x4>x1>x3,
故选:B.
点评 本题考查了二次方程的根,韦达定理,以及作差法比较大小,考查利用换元法进行变形能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.
如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 用水量y | 2.5 | 3 | 4 | 4.5 | 5.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
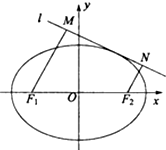 已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.
已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | C. | 向左平移2个单位 | D. | 向右平移2个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com