练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．在直角坐标系xOy中，圆C1和C2的参数方程分别是$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$（φ为参数）和$\left\{\begin{array}{l}x=cosβ\\ y=1+sinβ\end{array}\right.$（β为参数），以O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系；
    （1）求圆C1和C2的极坐标方程；
    （2）射线$OM：θ=α（0＜α＜\frac{π}{2}）$与圆C1的交点为O、P，与圆C2的交点为O、Q，求|OP|•|OQ|的最大值．

    分析 （1）圆C1的参数方程分别是$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$（φ为参数），利用平方关系可得普通方程，展开利用互化公式可得极坐标方程．圆C2的参数方程$\left\{\begin{array}{l}x=cosβ\\ y=1+sinβ\end{array}\right.$（β为参数），利用平方关系可得普通方程，展开利用互化公式可得极坐标方程．
    （2）把射线$OM：θ=α（0＜α＜\frac{π}{2}）$代入分别圆C1与圆C2的极坐标方程即可得出．

    解答 解：（1）圆C1的参数方程分别是$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$（φ为参数），
    利用平方关系可得普通方程：（x-2）2+y2=4，展开为：x2+y2-4x=0，
    可得极坐标方程：ρ2-4ρcosθ=0，即ρ=4cosθ．
    圆C2的参数方程$\left\{\begin{array}{l}x=cosβ\\ y=1+sinβ\end{array}\right.$（β为参数），
    利用平方关系可得普通方程：x2+（y-1）2=1，
    展开为：x2+y2-2y=0，可得极坐标方程：ρ2-2ρsinθ=0，即ρ=2sinθ．
    （2）把射线$OM：θ=α（0＜α＜\frac{π}{2}）$代入圆C1的极坐标方程可得：ρ1=4cosα．
    把射线$OM：θ=α（0＜α＜\frac{π}{2}）$代入圆C2的极坐标方程可得：ρ2=2sinα．
    |OP|•|OQ|=8cosα•sinα=4sin2α≤4，其最大值为4．

    点评 本题考查了极坐标方程化为直角坐标方程及其应用、参数方程化为普通方程、三角函数求值，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．已知函数f（x）的定义域为[-2，2]，且f（x）在[-2，2]上是增函数，f（1-m）＜f（m），则实数m的取值范围为（　　）
    A．$（\frac{1}{2}，+∞）$B．$（-∞，\frac{1}{2}）$C．$（{\frac{1}{2}，2}]$D．$[{-2，\frac{1}{2}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若函数f（x）在区间A上，对?a，b，c∈A，f（a），f（b），f（c）为一个三角形的三边长，则称函数f（x）为“三角形函数”．已知函数f（x）=xlnx+m在区间$[{\frac{1}{e^2}，e}]$上是“三角形函数”，则实数m的取值范围为（$\frac{{e}^{2}+2}{e}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设全集U=R，A={x|-2＜x＜1}，B={x|2x＞1}，则A∩（∁UB）=（　　）
    A．（0，1）B．（-2，0）C．（-2，0]D．（-2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．对?x∈（0，+∞）不等式（2x-2a+ln$\frac{x}{a}$）（-2x2+ax+5）≤0恒成立，则实数a的取值集合为{$\sqrt{5}$}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知函数f（x）=x+$\frac{a}{x}$（a＞0），若对任意的m、n、$p∈[\frac{1}{3}，1]$，长为f（m）、f（n）、f（p）的三条线段均可以构成三角形，则正实数a的取值范围是（$\frac{1}{15}$，$\frac{1}{9}$）∪[1，$\frac{5}{3}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．如图，在三棱柱ABC-A1B1C1中，M为A1C1的中点，若$\overrightarrow{AB}=\vec a$，$\overrightarrow{BC}=\vec b$，$\overrightarrow{A{A_1}}=\vec c$，则$\overrightarrow{BM}$可表示为（　　）
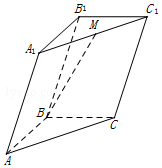
    A．$-\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$B．$\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$C．$-\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$D．$\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=x3+3x2-9x-3
    （Ⅰ）若函数f（x）在点（x0，f（x0））处的切线l与直线x-9y+1=0垂直，求切线l的方程；
    （Ⅱ）求函数f（x）的极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．我国古代数学著作《九章算术》有如下问题：“今有金杖，长五尺，斩本一尺，重四斤．斩末一尺，重二斤．问次一尺各重几何？”其大意是：“现有一根长五尺的金杖，一头粗，一头细．在粗的一端截下1尺重4斤．在细的一端截下1尺，重2斤．问依次每一尺各重多少斤？”根据上面的已知条件，若金杖由粗到细是均匀变化的，则金杖的质量为（　　）
    A．12斤B．15斤C．15.5斤D．18斤

    查看答案和解析>>

    同步练习册答案